• Supervised learning algorithm
• Used for regression and classification problems
• Decision tree-based ensemble learning algorithm
• Sequential ensemble learning
• Not require feature scaling
• It works well to use with an imbalance dataset
• Not sensitive to outliers
• Often slightly more accurate than random forests, slower to train but faster to predict than random forests, smaller in memory
• Gradient boosting strategically trains each new model to address the shortcomings of the previous ones

How It Works

1. Initialization:

• The ensemble starts with an initial model, often a simple one like a single-leaf tree or a constant value
• The initial prediction is made by this base model

2. Sequential Training:

For each iteration:

1. Compute the residuals: Calculate the difference between the actual target values and the predictions made by the current ensemble.
2. Create a new tree (Fit a base learner): Train a new weak learner (typically a decision tree) on the residuals. Fit the new model to predict the residuals, rather than the original target values.
3. Calculate the output values: In this part, we determine the output values for each leaf.
4. Make a new prediction: Update the ensemble by adding the new model's predictions scaled by a learning rate.
5. Repeat until a predefined number of iterations (trees) is reached or until a stopping criterion is met.

• Note: Gradient Boosting typically continues adding models until a predefined number of iterations is reached, or until the performance on a validation set fails to improve.

3. Combining Models:

• The final prediction is the sum of the initial prediction and the predictions from all subsequent models

Practical Example For Regression Problem

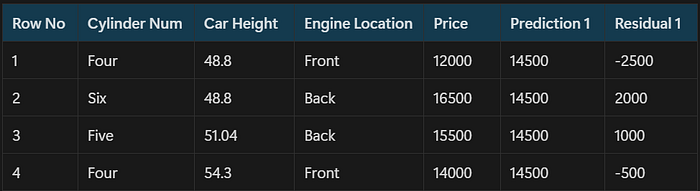
• Below is our raw data

Step-1: Build a Base Mode ⇒ We initialize the model with a constant value

Note:Our goal is to find the value for gamma(y_hat) to minimize the loss function, and we can find it below:

• For the value y_hat=14500, the loss function will be minimum, so this value will become our prediction for the base model

Step 2: is a loop where we make all of the trees (for m=1 to M)

• Little m refers to individual trees, so when m=1 we are talking about the first tree
• Step 2 consists of: Part(a), Part(b), Part(c), and Part(d)

Part(a): Calculate the pseudo residuals

• pseudo_residuals = (observed value — predicted value)

Note: We can prove that pseudo residuals are (observed value — predicted value) below:

• For m=1, the pseudo residuals are below:

Part(b): Fit a base learner hm(x)

• Let's say hm(x) is our DT (regressor tree) made on these residuals
• We will build a model on these pseudo residuals and make predictions. Why do we do this? Because we want to minimize these residuals and minimizing the residuals will eventually improve our model accuracy and prediction power
• So, using the Residual as a target and the original feature Cylinder number, cylinder height, and Engine location we will generate new predictions
• Note that the predictions, in this case, will be the error values, not the predicted car price values since our target column is an error now
• Here is our new tree

• The Residual for the first sample, x1, goes to the leaf on the left
• The Residual for the second and third samples, x2 and x3, goes to the leaf in the middle
• The Residual for the fourth sample, x4, goes to the leaf on the right

Part(c): In this part, we determine the output values for each leaf

• After training a decision tree to predict the pseudo-residuals, each instance will be assigned to a specific leaf node in the tree. It's possible that multiple instances end up in the same leaf node
• That means there might be a case where 1 leaf gets more than 1 residual, hence we need to find the final output of all the leaves. To find the output we can simply take the average of all the numbers in a leaf, doesn't matter if there is only 1 number or more than 1

Mathematically this step can be represented as below:

1. Let`s start by calculating the output value for the leaf on the left, R_1,1:

• j=1 → since it is the first leaf
• m=1 → since this is the first tree

2. Let`s start by calculating the output value for the leaf in the middle, R_2,1:

• j = 2 → since it is the second leaf
• m = 1 → since this is the first tree

• So the value for this equation to minimize that equation is 1500

3. Finally, let`s start by calculating the output value for the leaf on the right, R_3,1:

• j = 3 → since it is the second leaf
• m = 1 → since this is the first tree

Our DT after calculating the output of all the leaves is:

• That`s great! Now let`s jump to the next step 😎

Part(d): Update the model

• In this step, we have to update the predictions of the previous model. It can be updated as:

Now we will use F1(x) to make a new prediction for each sample:

• nu (learning rate)→ we will take 0.1 for this example

Below are our previous and current predictions for each sample:

• x1 => 14500 (Previous Prediction)=> 14250 (New Prediction)
• x2 => 14500 (Previous Prediction)=> 14650 (New Prediction)
• x3 => 14500 (Previous Prediction)=> 14650 (New Prediction)
• x4 => 14500 (Previous Prediction)=> 14450 (New Prediction)

Step-3: Output F_M(x)

• Imagine M=2
• In the below two images, the base model value is 73.3 and it is a different example from the one I used above
• In our example, the base model value was 14500
• For more clarity you can refer to the below images, to get to know the final step

• If we get new data, it will be predicted as below

How Gradient Boost Used For Classification:

• For using gradient boosting in classification problems, I recommend these two videos

1. First Video Link
2. Second Video Link

Advantages:

• High predictive accuracy
• Handles heterogeneous data
• Provides insight into feature importance
• Robustness to overfitting with proper tuning

Disadvantages:

• Computationally expensive due to sequential training
• Requires careful parameter tuning
• Sensitive to noisy data
• Models can be complex, making interpretation challenging

Python Implementation

# Gradient boost for regression problems
from sklearn.datasets import make_regression
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import train_test_split

X, y = make_regression(random_state=0)
X_train, X_test, y_train, y_test = train_test_split(
    X, y, random_state=0)
reg = GradientBoostingRegressor(random_state=0)
reg.fit(X_train, y_train)
reg.predict(X_test[1:2])
reg.score(X_test, y_test)
# Gradient boost for classificatoin problems
from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier

X, y = make_hastie_10_2(random_state=0)
X_train, X_test = X[:2000], X[2000:]
y_train, y_test = y[:2000], y[2000:]

clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
    max_depth=1, random_state=0).fit(X_train, y_train)
clf.score(X_test, y_test