This write-up discusses two concepts in context of Reinforcement Learning:

1. Difference between State Spaces and Observation Spaces.
2. State/ Observation Space & Action Space representation in OpenAI Gym.

A. Outline of Reinforcement Learning (RL)

Typical Reinforcement Learning (RL) Setup

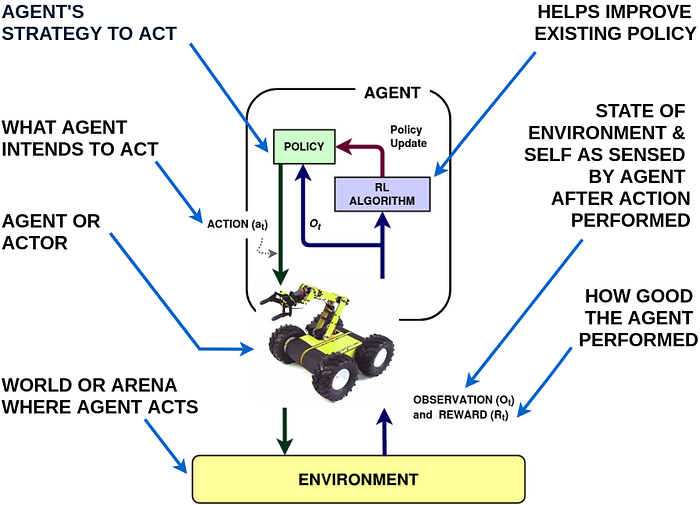
The above diagram introduces a typical setup of the RL paradigm. An Agent's (e.g. the yellow robot) goal is to learn the best possible way to perform a certain task in an Environment. The agent tries to achieve that task by taking actions (e.g. move left, right or stop) as suggested by a strategy (or Policy). So after it performs that specific action the agent observes the state of the environment (Observation) and a goodness score (or Reward) based on its last action. These feedback information are then utilized by the RL algorithm to upgrade/ improve the existing strategy (or policy), for better performance in the future. An agent can learn to play and win strategy games, e.g. Pacman (from Atari games), in which case the Pacman is an agent and the gaming construct is the environment. Following is an example (MountainCar-v0) from OpenAI Gym classical control environments. OpenAI Gym, is a toolkit that provides various examples/ environments to develop and evaluate RL algorithms. For details on installation and use of OpenAI Gym you can refer to these handy resources here & here.

About MountainCar-v0 : A car is on a one-dimensional track, positioned between two "mountains". The goal is to drive up the mountain on the right; however, the car's engine is not strong enough to scale the mountain in a single pass. Therefore, the only way to succeed is to drive back and forth to build up momentum. Lets connect the general RL terms learnt till now, in the context of this simple environment.

Agent: the under-actuated car . Observation: here the observation space in a vector [car position, car velocity]. Since this is a one dimensional problem, with a car moving on a curve like feature, its location is given by a continuous value between [-1.2,0.6] and the velocity is a bounded continuous value between [-0.07,0.07]. Reward: reward functions for these type of simulated environments are already built- in the environment code and in this case generates a reward = -1 for any transition from any state and reward=+100 when the agent reaches the objective (the flag). Action: the action space is discrete in this case and given as [Left, Neutral, Right]. Episode: A number of state and action sequence (~1000 in this case), along which the agent tries tries to complete the objective before re initiating . A trajectory may be defined as a part of a full episode and so every trajectory may not be a full episode.

So far we have learnt that a RL algorithm helps optimize/ improve a given policy while maximizing a given objective (i.e. the RL objective). The RL objective can be given as follows:

For an trajectory/ episode (τ) of length t = 1 to T, the cumulative reward (also called the Return ) calculated over all the state transitions over that length , is considered as the performance measure of that episode. The RL objective is that we need find the optimal policy parameter vector (φ*) that maximizes the expectation of the cumulative reward taken over all possible episodes. If the policy (which is a mapping between states and actions) is described as a probability distribution then φ represents the parameters (i.e.φ is the parameter vector) describing the policy. If the distribution is modeled using a neural network then φ represents the network weights.

B. How different are states and observation ?

1. The MDP and POMDP perspective:

Certain important terms. State: describes the state of the world or environment completely, e.g. a robot might have states like joint angles, velocity, position as the states defining it.

Complete Observation: when the agent is able to observe the complete state information that defines the status of the environment/ world after the agent has acted out a certain action, in it.

Partial Observation: when the agent is able to observe only partial information regarding the state of the environment.

Set of all States or the State Space can be considered same as the Observation space if the environment is completely observable (and without noise ). These completely observable RL cases are defined using the Markov Decision Process (MDP) framework.

As seen in the above illustration a MDP consists of 4 components < S,A,T,R> and they together can define any typical RL problem. The state space S is a set of all the states that the agent can transition to and action space A is a set of all actions the agent can act out in a certain environment. There are also Partial Observable cases, where the agent is unable to observe the complete state information of the environment. These cases are defined using Partially Observable MDP (POMDP). Here observation is introduced assuming the agent can see/sense/record only partial information of the environment states. The agent keeps an internal belief state, b, that summarizes its experience. The agent uses a state estimator, SE, for updating the belief state b, based on the last action. the current observation and the previous belief state.

2. Overlapping perspective of observation and state spaces :

The state space and observation space may as well overlap most importantly for the sake of convenience as in cases of most RL toy & simulated problems/ environments. The Gym environments are modeled as POMDPs (paper), which justifies using of the term 'observation' instead of 'state' and also essentially imply that the Gym environment is partially observed by the agent. But Gym does not provide any information regarding the actual or complete state space of any environment. So ultimately the observation space becomes a vector of all the states Gym uses to model an environment. Hence it might in a way appear like a MDP. Observation wrappers (check here) have been used to extend OpenAI Gym environments and turn them into truly Partially Observable Markov Decision Processes (e.g. here). Wrappers allows one to add functionality to environments, such as modifying observations, rewards and actions.

C. State/ Observation Spaces and Action Spaces

In most simulated environments/ test-beds/ toy problems the State space is equivalent to Observation spaces, as shown in above illustration. Both the state/observation and action spaces comes in both varieties (i.e. Discrete and Continuous). In the simplest of examples states/ observation constitutes only the position of the agent but with more complex and higher dimensional examples state/ observation space may constitute additional information (e.g. angular velocity, horizontal speed, position of joints etc.) or complex visual information like RGB matrix of observed pixel values e.g. in Gym Arcade games. In the GridWorld environment in Fig 4, the agent starts from the 'start' and uses RL ALgorithm ( based on Value Iteration, Policy Optimization etc. ) to reach the +1 rewarding box. The episode ends in case the agent reaches goal and obtains +1 reward or it reaches the -1 goal where it is rewarded -1. At every time step the agent is allowed to choose from a set of actions (the Action Space A) = [Right, Left, Up, Down] 𝝐 A. The decision on which action to take is either decided by a calculated value (e.g. in Value Iteration) or an iteratively evaluated and updated state-action mapping i.e. the Policy (e.g. in Policy Iteration). The next state resulting from an action by the agent is decided by the environment ( or its model/ the transition Probability ( T = p(s'|s,a) 𝝐 S )) (see Fig 3). The MountainCarContinuous-v0 environment, has a 2D state/ observation vector = [car position, car velocity], both these quantities are continuous in following ranges position = (-1.2,0.6), velocity = (-0.07, 0.07). The action space is 1D and consists of a continuous acceleration term, in the range = (-1,0,1.0).

D. State/ Observation Space and Action Space representation in Gym

I will briefly introduce the State/Observation and Action space representation in Gym platform. There are an ever increasing number of environments for developing and evaluating RL algorithms in OpenAI gym. Here & here you can find an exhaustive listing of available environments and their action and observation space information. Action and observation space information is very crucial for evaluation of Rl algorithms since many RL algorithms are developed only for specific type of State/ Observation and Action spaces. For example the DDPG algorithm can only be applied to environments with continuous action space, while the PPO algorithm can be used for environments with either discrete or continuous action spaces.

1. OpenAI Gym Toolkit- brief overview

The OpenAI Gym is a toolkit that serves as a test-bed for evaluating and comparing RL algorithms on various test problems called environment.

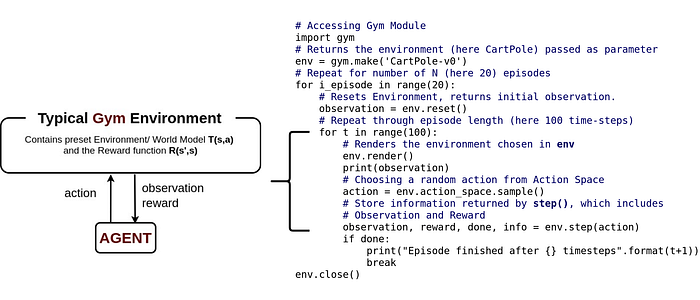
So given a RL algorithm that we intend to evaluate we choose a test example or environment of our choice from the Gym library (or other compatible libraries like Mujoco) and then we run the agent using that RL algorithm under evaluation. We can also collect the performance data of the RL algorithm and can plot or store them. Check here for familiarization with coding basics for Gym.

2. Observation and Action Spaces in Gym

There are currently 6 different types of spaces supported by OpenAI Gym. Following table explains each of these space types in details.

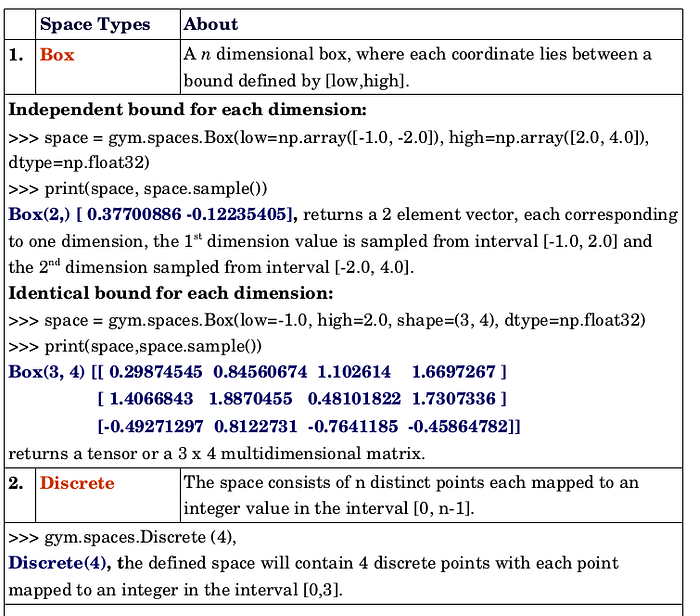
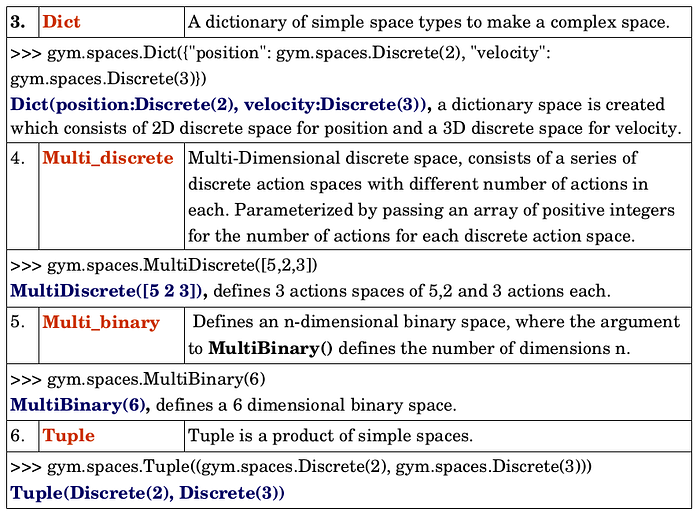
Box and Discrete are the two most commonly used space types, to represent the Observation and Action spaces in Gym environments. Apart from them there are other space types as given below

3. Querying details of Spaces of a Gym environment

For better understanding we would look into certain examples from Gym, that uses some of the above mentioned space types. Following is the queried space details for 4 such environments, namely MountainCar-v0, MountainCarContinuous-v0 (from Classical Control Environments) and LunarLander-v2, BipedalWalker-v2 (from Box2D Continuous Control tasks). The query returns the Observation space and Action space type. It also returns the High and Low values of the intervals, in the case of bounded continuous spaces.

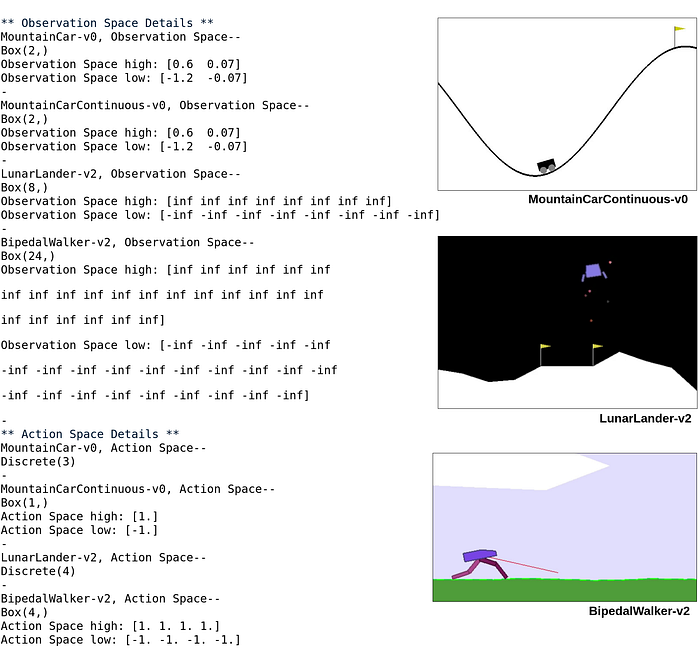
Information regarding the operation and setup of the above environments can be found here and here. The code used to query the observation and action space information is provided as a snippet as follows:

import gym
# Selecting environments
env01 = gym.make('MountainCar-v0')
env02 = gym.make('MountainCarContinuous-v0')
.
.
.
# Print Observation Space details -----------------------
print("** Observation Space Details **")
print("MountainCar-v0, Observation Space--\n" +str(env01.observation_space))
print("Observation Space high:" +str(env01.observation_space.high))
print("Observation Space low:" +str(env01.observation_space.low))
.
.
.
# Print Action Space space detail ------------------------
print("** Action Space Details **")
print("MountainCar-v0, Action Space--\n"+str(env01.action_space))
.
.
.

Lastly I hope that the above article was informative and has been able to clear some confusions regarding spaces of States, Observation and Action in RL literature and their representation & implementation in the OpenAI Gym API.