If you're learning algorithms or preparing for interviews, you've likely encountered Big O Notation. It's a fundamental concept for understanding how efficient (or inefficient) your code is — especially as the size of input data grows. 📈

In this post, we'll break down Big O Notation using real-world Java examples and a visual diagram to help you remember them better.

🔍 What is Big O Notation?

Big O describes the upper bound of an algorithm's running time or space complexity as the input size n increases. It helps you focus on the growth rate rather than exact performance.

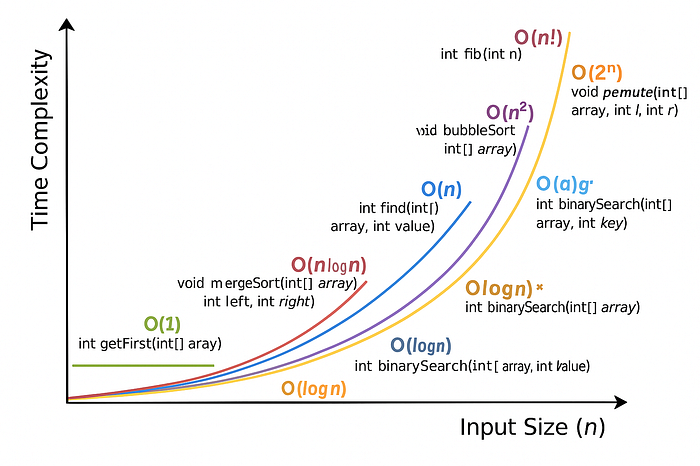
📊 Visual Guide to Big O

Below is a custom graph showing how each time complexity grows as input increases. Notice how steep the curves get for O(n²), O(2ⁿ), and O(n!) compared to the more efficient O(log n) and O(n).

📦 Java Code Snippets

// O(1)
int getFirst(int[] arr) {
    return arr[0];
}

// O(n)
int find(int[] arr, int value) {
    for (int i : arr) {
        if (i == value) return i;
    }
    return -1;
}

// O(log n)
int binarySearch(int[] arr, int value) {
    int low = 0, high = arr.length - 1;
    while (low <= high) {
        int mid = (low + high) / 2;
        if (arr[mid] == value) return mid;
        else if (arr[mid] < value) low = mid + 1;
        else high = mid - 1;
    }
    return -1;
}

// O(n²)
void bubbleSort(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
        for (int j = 0; j < arr.length - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

✅ Conclusion

Big O Notation gives you a powerful lens to evaluate and improve your code. When coding in Java (or any language), always aim for better complexity. Avoid O(n²) or worse unless absolutely necessary, and optimize for O(log n) or O(n) wherever possible. 🧠