Singular Value Decomposition (SVD) is a frequently used concept in Data Science, Computer Vision and Artifical Intelligience. SVD is one key component to understanding Structure from Motion too. However SVD is quite a foreign concept to grasp, espically if you do not have a full background in Linear Algebra. No worries, you can do micro-learning to grasp all the concepts u need to data science. This story first explain what is a rank of matrix, then explain the Structure From Motion problem and then uses the rank of a matrix and SVD in to solve the Structure from Motion problem.
Rank of Matrix
Firstly, a matrix is just made up of a list of component vectors. If we group the matrix by rows, thematrix is made up of a list of multiple row vectors. If we group by columns, the matrix is made up of a list of multiple column vectors. For the rest of the story, we will explain concepts using column vector.

The rank of the matrix is the least number of its component vectors that can be used to derive all of its component vectors. Seems hard to understand? We first look at a matrix as a list of multiple column vectors. From left to right, we ask if each column vector can be derived from any of the column vector before it. The first column vector will always be NO as there are no column vectors before it. The second vector and beyond will depends if it can be derived from a linear combination of vector(s) before it. See the diagrams below and the rank of each matrix will be number of NO(s) as it is the minimum number of component vectors that can be used to derive all other component vectors in the matrix.

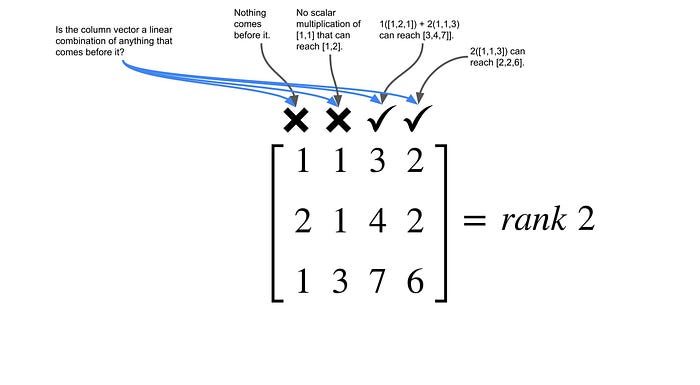
What is the meaning of the rank of a matrix? The rank of the m x n matrix enable the matrix to be represented by vectors that are less than n size. For example, if we re-write the above 4x4 matrix as column vectors, c1, c2, c3, c4, the matrix can be re-represented as a linear combination of first two vectors.
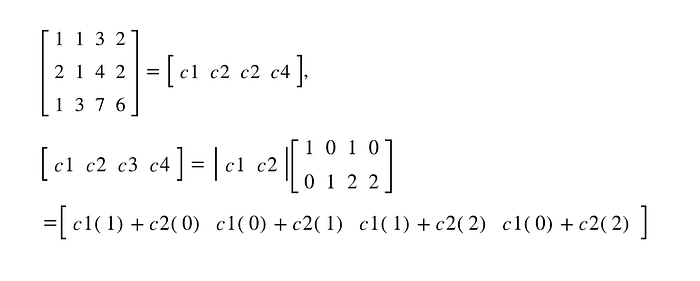
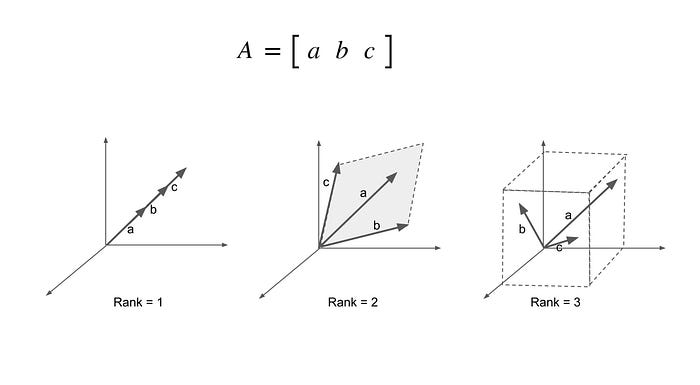
We can also visualise the rank of a matrix geometrically. Supposed we have a matrix of column vectors a, b and c. If the matrix is rank 1, vector a, b, and c are co-linear, which means they lie on the same line. You need just a scalar mutiplication of one of the vector to derive the other vectors. If the matrix is rank 2, vector a, b, and c are co-planar, which means they lie in the same plane. You need a linear combination of at least two vectors to derive any vector in the plane. If a matrix is rank 3, you need a linear combination of at least three vectors to derive any vector in the three dimension space.
Properties of rank of matrix:
Rank of m x n Matrix A ≤ min(m, n)
Rank of AB ≤ min(rank of A, rank of B)
Structure From Motion
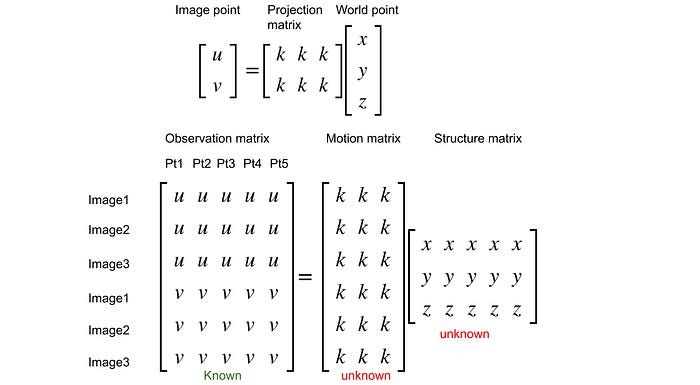
Lets understand the Structure From Motion problem before solving it with SVD. Structure From Motion is to take a sequence of 2D images of a 3D object and from the sequnce of 2D images, we recover the 3D points of the object, along with the camera motion. Imagine we took 3 consecutive images of a statue at three different positions. Each image contains five image points, that correspond to the same five points of the statue.
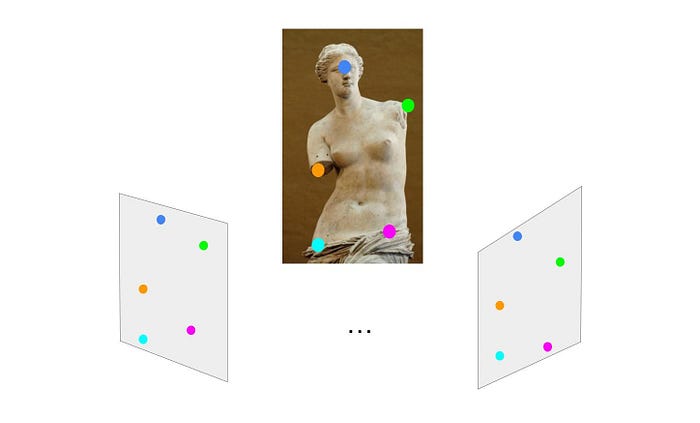
Let us simply the problem to that we can focus on bringing the solution to SVD later on. Lets say an image point (u,v) is the projection of world point (x,y,z) and a 2x3 Projection Matrix map the world point to image point. We can then form the 6x5 Observation Matrix, recording all the image points taken from all three images. We also know that the observation matrix can be decompose to the 6x3 Motion Matrix (similar to Projection Matrix) and the 3x5 Structure Matrix (five world points). The Observation Matrix is known, which are the 15 image points from three images while the Motion Matrix and Structure Matrix are unknown. Getting the Structure Matrix give us the five world points of the statue which can help us re-construct the 3D statue digitally. Getting the Motion Matrix will help us find where are the positions of cameras. Since the rank of Observation Matrix is less than or equal to the rank of Motion Matrix (3) and rank of Structure matrix (3), the Observation Matrix have a rank of ≤ 3. This large matrix with low rank is what can be exploited in the next step SVD to solve for the Motion Matrix and Structure Matrix.
SVD
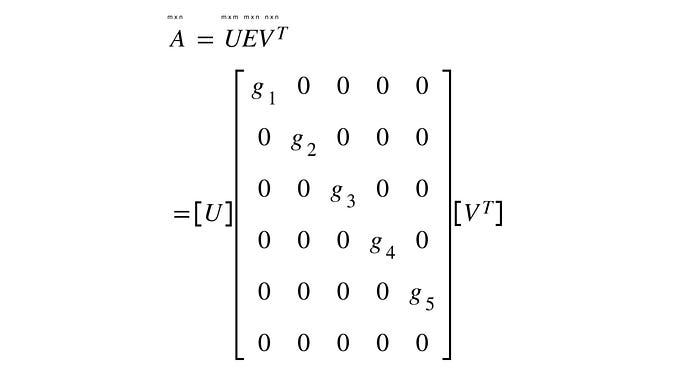
Every m x n matrix can be decomposed by SVD to three separate matrixes, U (m x m), E (m x n), Vtransposed (n x n). This decomposition is usally done with the help of computer algorithms that will not be elaborated as the purpose is to understand the outcome and usage of the decomposition. E is a diagonal matrix, which means only the diagonal of the matrix have non-zero values. The diagonal values, g1-g5, are also known as the singular values. g1-g5 are also in descending order, meaning g1 is the largest. This would means tha rows of U and columns of V that is multiplied by g1 will have the largest contribution to reconstruct matrix A. The opposite is true for g5.
Taking the Observation Matrix as A for example, SVD of A will result in a 6x6 matrix U, 6x5 diagonal matrix E, and 5x5matrix Vtranposed. Since we know that the Observation Matrix has a rank ≤ 3, only the first three diagonal values of E will have non-zero values. This would also mean only U1 of U and VT1 of Vtransposed would be useful in reconstructing the Observation Matrix. Hence, the Observation Matrix could be decomposed to a 6x3 matrix U, 3x3 diagonal matrix E, and 3x5matrix Vtranposed.

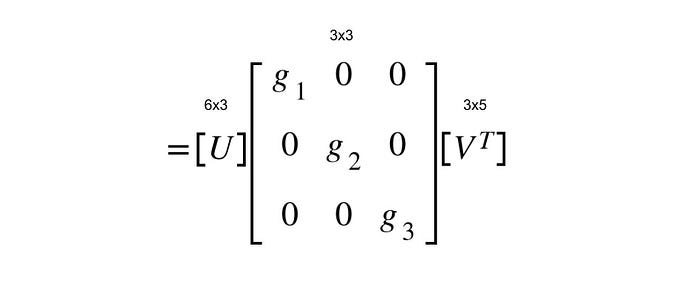
To get the Motion Matrix and Structure Matrix from the three matrixes after SVD, we can use factorization. Below gives an example of near-final factorization of the three matrixes after SVD to Motion Matrix and Structure Matrix but it is not the final factorization to Motion Matrix and Structure Matrix. The method just split diagonal matrix E into two square roots of E and muliple each square root to U and Vtransposed respectively. We will not go into the final solution of Motion Matrix and Structure Matrix as this story concentrate on helping people better undersand rank of matrix, SVD and its usage in Structure from Motion.

Thanks https://www.youtube.com/watch?v=2ogdwpHD3V8&list=LL&index=2 and https://www.youtube.com/watch?v=Lyd7cf0agvI&list=PL2zRqk16wsdoYzrWStffqBAoUY8XdvatV&index=11 for helping me understand the concepts!

