Have you ever found yourself packing for a trip, weighing the necessity of each item? What did you decide to leave behind?

So, suppose you are packing for a hiking trip where you need to limit the weight of your backpack.

You have several essential items, like water and food, and others that are nice-to-haves, like a pen or a book. The goal is to minimize the weight while keeping what's necessary to enjoy the hike.

In Lasso Regression (Aw, we aren't really going for a hike!), coefficients are the "items," and we try to minimize the weight of our model. If a feature doesn't add much value (like the book),

If you are not a member, check the article here: Finding the Right Balance: Better Choices with Lasso Regression!

Lasso Regression

Lasso, which stands for Least Absolute Shrinkage and Selection Operator, adds a unique penalty to the regression model.

Like Ridge regression, it includes a regularization term to keep the coefficients under control. Still, here, the penalty is the sum of the absolute values of the coefficients rather than their squares.

This difference allows Lasso to do something unique: it can shrink some coefficients to zero, effectively selecting only the most relevant features in the model.

Linear Regression and the Need for Lasso

In Linear Regression, we minimize the sum of squared residuals (SSR), aiming for a line that best fits all data points. However, this can lead to overfitting, especially with complex datasets.

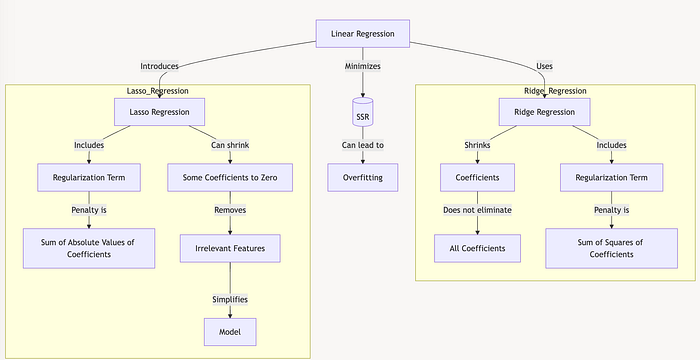
Ridge Regression addresses this by shrinking the coefficients through a penalty, but it doesn't eliminate them.

Enter Lasso Regression, which reduces some coefficients to zero, removes irrelevant features, and simplifies the model.

This approach can make the model more interpretable by focusing only on the core predictors.

How Lasso Regression Works

In Lasso Regression, the goal is to minimize the cost function with an added penalty term:

Cost Function for Lasso:

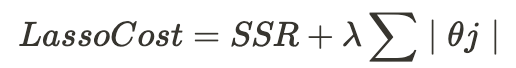
Where:

• The first term, SSR, is the same as in Linear Regression, which is the error term.
• ∑∣θj​∣ is the L1 penalty on the coefficients that sum up the absolute values of the coefficients.
• λ is the regularization parameter.

Here, λ (lambda) controls the strength of the penalty. With a higher λ, Lasso applies more pressure to the coefficients, possibly shrinking some of them to zero.

This penalty term leads Lasso to automatically select features that matter most, discarding others by setting their coefficients to zero.

Example: Predicting House Prices with Lasso

Let's say you have a dataset predicting house prices based on multiple features, like house size, number of rooms, and neighbourhood quality. Some of these features might not contribute significantly to predicting the price.

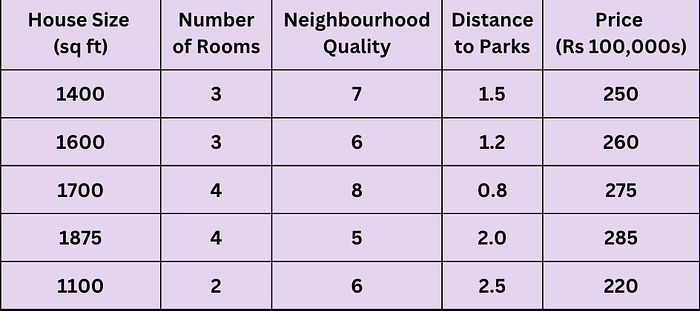
Step 1: Standardise the Dataset

Before applying Lasso, we standardize each feature to have a mean of 0 and a standard deviation of 1. This ensures that the penalty λ affects all features equally.

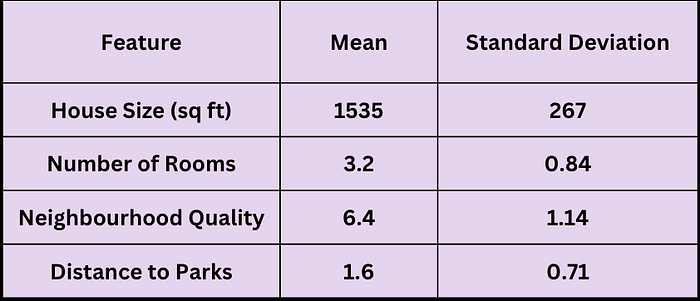
Standardized Dataset

The standardized dataset (with mean 0 and standard deviation 1) looks as follows:

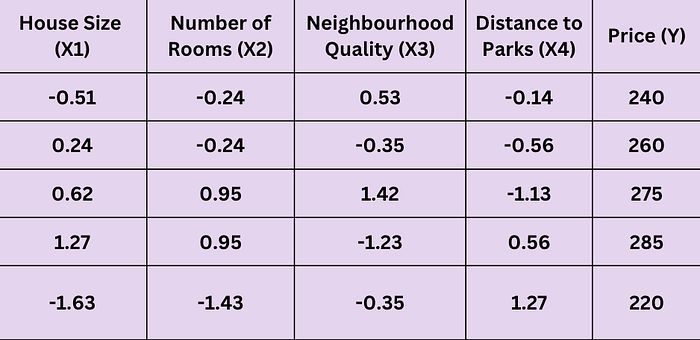
Step 2: Set Up the Lasso Cost Function

The Lasso cost function for this setup is:

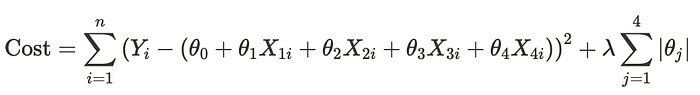
Let's set a small λ value, say λ = 0.5, to see its effect on feature selection.

Step 3: Calculate Initial Coefficients Using Linear Regression

Using ordinary least squares (OLS), we first calculate initial coefficients (without regularization) as a baseline.

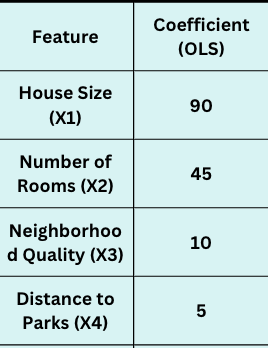
Step 4: Apply Lasso Penalty

Now, we adjust each coefficient using Lasso's soft-thresholding rule to determine the new values. The soft-thresholding rule for each coefficient θj\theta_jθj with Lasso is:

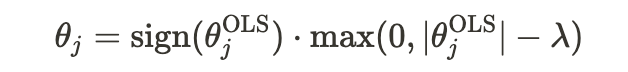
Calculating the Adjusted Coefficients

1. House Size (X1):

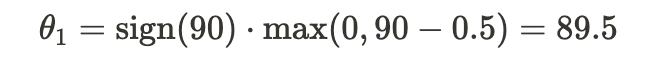
2. Number of Rooms (X2):

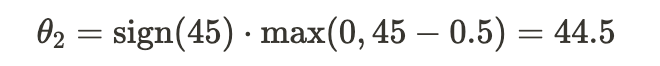
3. Neighborhood Quality (X3):

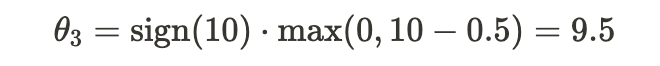
4. Distance to Parks (X4):

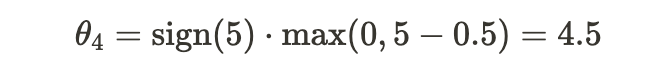
Step 5: Interpretation of Results

After applying the Lasso penalty, we see the coefficients slightly reduced:

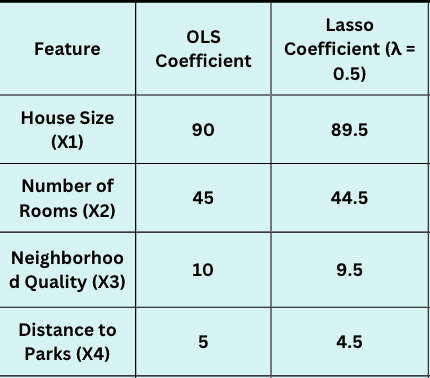
In this small λ example, Lasso hasn't zeroed out any coefficients because λ isn't large enough. However, as we increase λ, the less impactful features, like Neighbourhood Quality and Distance to Parks, may reduce to zero if they do not contribute significantly to the prediction.

Wrapping Up

Lasso Regression is like finding the perfect angle along with the right pull on the bowstring — it helps your model focus on the essentials, ignoring distractions.

With Lasso, you can achieve a more streamlined model that's easier to interpret and less prone to overfitting. It's precious when you have many predictors and want a model that highlights only the core insights in your data.