In recent years, a powerful alliance has been forged between the transformer neural network architecture and the formulation of various problems as self-supervised sequence prediction tasks. This union has enabled researchers to train large foundation models of unprecedented sizes using massive troves of unlabeled sequential data, and these models have shown uncanny emergent capabilities that closely mimic human-level intelligence in several domains. With newfound heights of practical utility unleashed, artificial intelligence (AI) was catapulted into mainstream life and conversation, and few today are unaware that the once fictional realm of silicone-based intelligence has now become very tangible and real.

However, intrinsically linked to the explosive growth in AI capabilities has been the rapid inflation of model sizes well into the hundreds of billions (and in some cases trillions) of parameters. A powerful new technology was delivered to the world, but it could be only be served using massive hardware clusters. Echoing the challenges from earlier eras of AI, the temptation to possess these powers on consumer hardware or edge devices was tremendous, and motivation to compress these pretrained behemoths took effect immediately, triggering catalytic flows of funding and talent into the study of model compression, and reanimating several well-pedigreed techniques including pruning, quantization, knowledge distillation, and parameter-efficient fine-tuning.

In part one of the Streamlining Giants series, we began our discussion on democratizing the power of large language models (LLMs) through model compression by exploring the rich legacy of research in neural network pruning, from its inception through its recent applications in LLMs containing tens or hundreds of billions of parameters. Along the way, we discovered that these large models can be compressed substantially with minimal drops in performance and marked gains in computational burden through either the unstructured or structured removal of the least important parameters from the network. We also saw that while pruning produces compact models that can operate in resource-constrained environments, the process itself traditionally required calculation of gradient information and/or retraining of the model to recover performance. This meant that the method was historically only accessible for those with the computational resources needed to train the original model, which in the case of LLMs would mean millions of dollars. While this originally placed the means of compressing models through pruning outside of the reach of those who needed it most, we saw that recent studies have proposed highly accessible methods using low-rank gradients or even just forward-pass information. Further, with the retraining of large models facilitated by simultaneous advances in parameter-efficient fine-tuning methods, pruning can now be performed using consumer hardware.

In this installment, we investigate an orthogonal approach to model compression: Quantization seeks to improve the computational efficiency and memory requirements of models by reducing the precision of the numbers being stored and operated on by the network, which may include the weights, activations, or both. While quantization can refer to any drop in precision, for example from 32-bit to 16-bit floating point, it also often involves a transition into the integer space, which offers accelerated operation and deployment on consumer hardware. As we will see, quantization is an extremely powerful method for compressing LLMs, offering significant reductions in computational overhead and hardware requirements with only minor or even non-existent drops in performance, making it the most widely employed model compression technique in today's world of large models. Further, by varying the levels of numeric precision, we can tune the accuracy/efficiency tradeoff for our use case.

Along this journey, we will see that quantization works in harmony with the pruning techniques we encountered previously, as well as with knowledge distillation and parameter-efficient fine-tuning methods which we have yet to explore, providing us a glimpse into the upcoming topics of investigation in the Streamlining Giants series. There is a popular adage which states that "there is no such thing as free lunch," but as we saw in our investigation into pruning: when it comes to model compression, sometimes there is. Similar to pruning, quantization acts as a form of regularization which is known to make neural networks more robust and generalizable, meaning that judicious applications of these techniques can often simultaneously compresses a model and improve its performance. In this article, we will survey the literature and see several examples of "free lunch" compression. By the end, even the skeptical reader should find themselves disabused of the notion that network quantization inherently suggests a degradation in quality. After reviewing the research, we will explore the tools for applying these techniques in our own work using open-source software. Now, let us dig in to the exciting field of neural network quantization.

Note: For those who want to skip the lesson and get straight to the implementation guide for accelerating their workflows, click here.

Quantization

As a testament to the success and necessity of quantization in LLM deployment, every popular open-source LLM serving solution today provides ready access to quantized models, which are often the default selections. The popular Ollama, for instance, which I recently had a great deal of fun using to create an open-source speech-to-speech multilingual language learning assistant, is built on top of llama.cpp, a pure C/C++ library developed to make the optimized deployment of quantized LLMs on consumer hardware a reality. For real-time vision-language applications like robots using low-power hardware, deploying quantized models with these types of hardware-optimized serving backends is imperative. But what exactly is quantization, and what makes it so effective at compressing neural networks?

Quantization refers to the mapping of a continuous real-number space into a fixed set of discrete numbers, or more broadly, to the transition of any numeric space into a lower-precision representation. Take for instance the 32-bit "single" or "full" precision floating point value, or even the high-resolution 64-bit "double" float; both of these data types have a limited precision in the number of decimal places they can carry. Therefore, they are examples of quantized distributions, since there are an infinite number of values between each of the "steps" in their final decimal place which cannot be represented, creating the distinct "staircase" pattern of the digital world. Indeed, the challenge of effectively manipulating continuous values in a discrete system are as old as digital computer science itself. Even floating-point numbers are decomposed into integers under the hood, since digital computers process binary information, which is inherently discrete. Therefore, when it comes to neural networks, the question is technically not "is it quantized," but rather "how quantized is it?"

Unlike other applications of quantization, such as signal processing, where the objective is strictly to have the quantized numbers represent their original values as closely as possible, the end goal in neural network quantization is to discretize the parameters in such a way that lowers their precision as much as possible while maintaining the same output from their collective interoperation. Since neural networks are highly overparameterized, and therefore have entire manifolds of optima in their loss gradient space that contain many possible solutions, the individual weights are free to move relatively far from their original values during quantization as long as their collective interaction stays on this solution manifold, providing the opportunity to optimize the model parameters with their subsequent quantization in mind, known as Quantization-Aware Training (QAT).

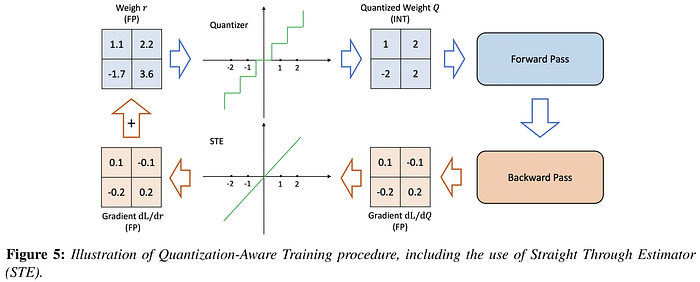
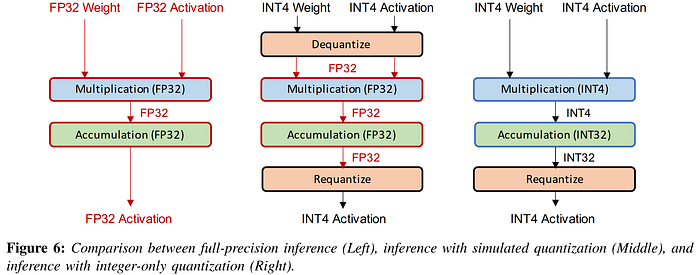
Performing QAT is often done using simulated or fake quantization, where parameters are stored in low-precision, but the operations are still carried out using floating point arithmetic. In the case of QAT, performing the math in floating point provides the conditions for gradient descent (along with the Straight Through Estimator or "STE", which simply ignores the destructive effect of the rounding function on the gradient), but some methods will also use simulated quantization at inference time when they focus on storage efficiency rather than runtime acceleration.

Simulated quantization stands in contrast to integer-only or fixed-point quantization, in which all operations are performed using low-precision arithmetic. Integer-only quantization is generally where the full advantages in latency and power consumption reside, but considerations will vary depending on hardware, as modern GPUs have highly optimized floating point units, while edge devices use low-power hardware where integer arithmetic may be more efficient. The use of simulated or integer-only quantization depends on the use case; for instance, simulated quantization would be a good choice for iteratively testing the sensitivity of different network components to varying levels of quantization without worrying about the hardware implementation, while integer-only quantization is likely to be the best choice for optimized deployment at the edge.

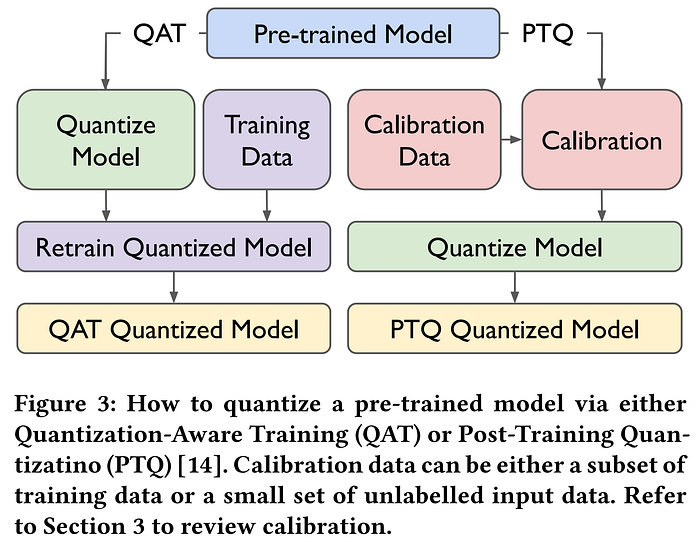
While QAT produces optimal results by factoring the quantization effects into the training process, it is met with the same challenge we encountered previously during our pruning investigation: if we seek to compress very large models like LLMs, we sincerely want to avoid a retraining phase for several reasons, including not having access to the training data, or not wanting to spend millions of dollars on the GPU hours required. For this reason, we are driven to abandon the understandably superior results of QAT, and look instead to Post-Training Quantization (PTQ) methodology, which requires only a small set of calibration data, and ultimately hope for the success of Zero-Shot Quantization (ZSQ) methods, which explore the ideal scenario of using no data at all. As we will see, recent work has pushed PTQ to impressive levels of accuracy, closely matching full precision baselines even in low-bit settings, and has become very accessible thanks to the efforts of open-source research and code.

The benefits of quantizing neural networks extend beyond compression. Like pruning, quantization acts as a form of regularization in neural networks by reducing the number of unique parameters, and therefore can also lead to increased performance and generalization capability when applied judiciously. In this way, quantization joins pruning as another "free lunch" compression method for neural networks, as the substantial reductions in model size and complexity can also paradoxically provide improved performance (when tuned correctly). Given the benefits of discretization, it starts to appear that the representation of neural networks in floating point is merely a larval stage of development required only for creating the mathematical conditions conducive to gradient descent during training, and that the subsequent quantization is not just a post-processing technique for model compression, but is actually an essential maturation stage in the neural network development lifecycle. Further, if research trends continue, equivalent training results may eventually be achieved using optimized integer-only math, which could free us from the need of high-precision neural networks forever.

Quantization touches every part of LLM development, from training to deployment, and encompasses a broad range of techniques which aim to reduce the memory, power, and computational efficiency of large models. For example, it has become common practice to train LLMs in mixed precision, where less-sensitive calculations are carried out in half-precision (16-bit float) rather than full 32-bit floating point precision, dramatically reducing their size in memory and the power required to operate on them without significantly affecting results. Modifications such as this not only allow us to iterate and develop models more freely, but they also have broad environmental implications at the scale of large model training, which can be measured in tons of CO2 in the case of LLMs.

Truly, when equivalent mathematical outcomes can be reached using a fraction of the resources, there are no losers, and very big gains to be made. This promise has inspired a formidable corpus of research in neural network quantization spanning several decades, and continuing to gain momentum even as we speak, which means that while this exploration aspires to be comprehensive and self-contained, we will have to round off some detail in order to fit it into memory. Ambitious readers should refer to the recent and comprehensive Gholami et al. 2021 survey, or to the Gray & Neuhoff 1998 survey for a more historically focused perspective.

Outline

Attempting to provide the shortest route to an informed understanding of the topic of neural network quantization, the remainder of the article will proceed as follows: first, we familiarize ourselves with the mathematics underlying quantization so that we are grounded in our discussion. Then, we discover the roots of neural network quantization research in the early 1990s, and connect them to the later efforts during the "deep learning revolution" that followed the seminal success of AlexNet on the image classification task in 2012. Accordingly, we will witness quantization research in the modern era proliferate first in computer vision and subsequently take hold in natural language processing, at which point we will be prepared to discuss the applications of quantization in today's world of LLMs, and discover the best libraries and tools for incorporating these methods into our workflows. Finally, we will reflect on our findings, and discuss directions for future work.

This article is organized in chapters so that it can be read in clearly defined pieces. The reader may choose to skip sections if they are in a hurry to find information, but keep in mind that the terminology encountered may be defined in earlier chapters. Together, these sections compose a reasonably self-contained review on the subject of neural network quantization, and it aspires to equip ML practitioners from enthusiast through professionals with a depth of knowledge which will enable them to optimize their own workflows. The article concludes with an implementation guide for LLM quantization, and time-constrained readers can skip directly there.

1. The Mechanics of Quantization a. Bit Width b. Uniform Quantization c. Non-uniform Quantization d. Mixed-precision Quantization e. Scalar vs. Vector Quantization f. Compensating for the Effects of Quantization
2. The History of Neural Network Quantization a. Early Work in Neural Network Quantization b. Quantization in the Post-AlexNet Era • Quantization-Aware Training of CNNs • The Rise of Mixed-Precision Quantization • Post-Training Quantization of CNNs • Extreme Quantization: Binary and Ternary Networks
3. Quantization of LLMs a. Quantization in the Early Era of Transformers b. Post-training Quantization of LLMs c. Quantization-Aware Training of LLMs • Extreme Quantization of LLMs
4. Practitioner's LLM Quantization Guide a. LLM Quantization Decision Tree
5. Conclusion a. Future Work

The Mechanics of Quantization

To ground our investigation into quantization, it is important to reflect on exactly what we mean by "quantizing" numbers. So far we've discussed that through quantization, we take a set of high-precision values and map them to a lower precision in such a way that best preserves their relationships, but we have not zoomed into the mechanics of this operation. Unsurprisingly, we find there are nuances and design choices to be made concerning how we remap values into the quantized space, which vary depending on use case. In this section, we will seek to understand the knobs and levers which guide the quantization process, so that we can better understand the research and equip ourselves to bring educated decision making into our deployments.

Bit Width

Throughout our discussion on quantization, we will refer to the bit widths of the quantized values, which represents the number of bits available to express the value. A bit can only store a binary value of 0 or 1, but sets of bits can have their combinations interpreted as incremental integers. For instance, having 2 bits allows for 4 total combinations ({0, 0}, {0, 1}, {1, 0}, {1, 1}) which can represent integers in the range [0, 3]. As we add N bits, we get 2 to the power of N possible combinations, so an 8-bit integer can represent 256 numbers. While unsigned integers will count from zero to the maximum value, signed integers will place zero at the center of the range by interpreting the first bit as the +/- sign. Therefore, an unsigned 8-bit integer has a range of [0, 255], and a signed 8-bit integer spans from [-128, 127].

This fundamental knowledge of how bits represent information will help us to contextualize the numeric spaces that the floating point values get mapped to in the techniques we study, as when we hear that a network layer is quantized to 4 bits, we understand that the destination space has 2 to the power of 4 (16) discrete values. In quantization, these values do not necessarily represent integer values for the quantized weights, and often refer to the indices of the quantization levels — the "buckets" into which the values of the input distribution are mapped. Each index corresponds to a codeword that represents a specific quantized value within the predefined numeric space. Together, these codewords form a codebook, and the values obtained from the codebook can be either floating point or integer values, depending on the type of arithmetic to be performed. The thresholds that define the buckets depend on the chosen quantization function, as we will see. Note that codeword and codebook are general terms, and that in most cases the codeword will be the same as the value returned from the codebook.

Floating-Point, Fixed-Point, and Integer-Only Quantization

Now that we understand bit widths, we should take a moment to touch on the distinctions between floating-point, fixed-point, and integer-only quantization, so that we are clear on their meaning. While representing integers with binary bits is straightforward, operating on numbers with fractional components is a bit more complex. Both floating-point and fixed-point data types have been designed to do this, and selecting between them depends on both on the deployment hardware and desired accuracy-efficiency tradeoff, as not all hardware supports floating-point operations, and fixed-point arithmetic can offer more power efficiency at the cost of reduced numeric range and precision.

Floating-point numbers allocate their bits to represent three pieces of information: the sign, the exponent, and the mantissa, which enables efficient bitwise operations on their representative values. The number of bits in the exponent define the magnitude of the numeric range, and the number of mantissa bits define the level of precision. As one example, the IEEE 754 standard for a 32-bit floating point (FP32) gives the first bit to the sign, 8 bits to the exponent, and the remaining 23 bits to the mantissa. Floating-point values are "floating" because they store an exponent for each individual number, allowing the position of the radix point to "float," akin to how scientific notation moves the decimal in base 10, but different in that computers operate in base 2 (binary). This flexibility enables precise representation of a wide range of values, especially near zero, which underscores the importance of normalization in various applications.

In contrast, "fixed" point precision does not use a dynamic scaling factor, and instead allocates bits into sign, integer, and fractional (often still referred to as mantissa) components. While this means higher efficiency and power-saving operations, the dynamic range and precision will suffer. To understand this, imagine that you want to represent a number which is as close to zero as possible. In order to do so, you would carry the decimal place out as far as you could. Floating-points are free to use increasingly negative exponents to push the decimal further to the left and provide extra resolution in this situation, but the fixed-point value is stuck with the precision offered by a fixed number of fractional bits.

Integers can be considered an extreme case of fixed-point where no bits are given to the fractional component. In fact, fixed-point bits can be operated on directly as if they were an integer, and the result can be rescaled with software to achieve the correct fixed-point result. Since integer arithmetic is more power-efficient on hardware, neural network quantization research favors integer-only quantization, converting the original float values into integers, rather than the fixed-point floats, because their calculations will ultimately be equivalent, but the integer-only math can be performed more efficiently with less power. This is particularly important for deployment on battery-powered devices, which also often contain hardware that only supports integer arithmetic.

Uniform Quantization

To quantize a set of numbers, we must first define a quantization function Q(r), where r is the real number (weight or activation) to be quantized. The most common quantization function is shown below:

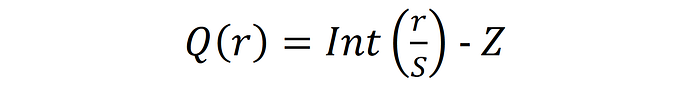
In this formula, Z represents an integer zero-point, and S is the scaling factor. In symmetrical quantization, Z is simply set to zero, and cancels out of the equation, while for asymmetrical quantization, Z is used to offset the zero point, allowing for focusing more of the quantization range on either the positive or negative side of the input distribution. This asymmetry can be extremely useful in certain cases, for example when quantizing post-ReLU activation signals, which contain only positive numbers. The Int(·) function assigns a scaled continuous value to an integer, typically through rounding, but in some cases following more complex procedures, as we will encounter later.

Choosing the correct scaling factor (S) is non-trivial, and requires careful consideration of the distribution of values to be quantized. Because the quantized output space has a finite range of values (or quantization levels) to map the inputs to, a clipping range [α, β] must be established that provides a good fit for the incoming value distribution. The chosen clipping range must strike a balance between not over-clamping extreme input values and not oversaturating the quantization levels by allocating too many bits to the long tails. For now, we consider uniform quantization, where the bucketing thresholds, or quantization steps, are evenly spaced. The calculation of the scaling factor is as follows:

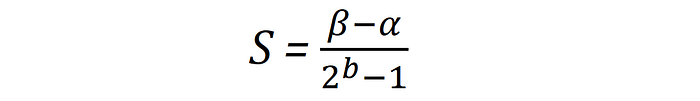
The shapes of trained parameter distributions can vary widely between networks and are influenced by a number of factors. The activation signals generated by those weights are even more dynamic and unpredictable, making any assumptions about the correct clipping ranges difficult. This is why we must calibrate the clipping range based on our model and data. For best accuracy, practitioners may choose to calibrate the clipping range for activations online during inference, known as dynamic quantization. As one might expect, this comes with extra computational overhead, and is therefore by far less popular than static quantization, where the clipping range is calibrated ahead of time, and fixed during inference.

Dequantization Here we establish the reverse uniform quantization operation which decodes the quantized values back into the original numeric space, albeit imperfectly, since the rounding operation is non-reversible. We can decode our approximate values using the following formula:

Non-Uniform Quantization

The astute reader will probably have noticed that enacting uniformly-spaced bucketing thresholds on an input distribution that is any shape other than uniform will lead to some bits being far more saturated than others, and that adjusting these widths to focus more bits in the denser regions of the distribution would more faithfully capture the nuances of the input signal. This concept has been investigated in the study of non-uniform quantization, and has indeed shown benefits in signal fidelity; however, the hardware-optimized calculations made possible by uniform quantization has made it the de-facto neural network quantization method. The equation below describes the non-uniform quantization process:

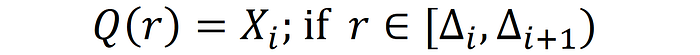
Many works in non-uniform quantization refer to learning centroids, which represent the centers of clusters in the input distribution to which the surrounding values are mapped through the quantization process. To think of this another way, in uniform quantization, where the thresholds are evenly spaced on the input distribution, the centroids are simply the values directly in between the bucketing thresholds.

Mixed-Precision Quantization

As we saw with pruning, a trained neural network's performance is more sensitive to changes in some layers and submodules than others, and by measuring these sensitivities, entire pieces of neural networks can be removed without significantly affecting error. Intuitively, the same is true for varying levels of quantization, with some network components capable of being remapped to much lower bit widths than their counterparts. The most fundamental example of this we already mentioned: the use of 16-bit floats in less-sensitive network operations to substantially reduce memory footprint during training, but mixed-precision quantization can refer to any combination of different quantization levels throughout a network.

Related to the concept of mixed-precision quantization is the granularity of quantization, which might be layer-wise, group-wise, channel-wise, or sub-channel-wise, and describes the scale at which distinct sets of quantization parameters are calibrated. Intuitively, computational overhead increases with granularity, representing an accuracy/efficiency trade-off. For example, in convolutional neural networks (CNNs), channel-wise granularity is often the weapon of choice, since sub-channel-wise (i.e. filter-wise) quantization would be too complex.

Scalar vs. Vector Quantization

While the majority of research in quantization has historically focused on quantizing individual values within the matrices, it is possible to learn multidimensional centroids as well. This means that matrices can be split into vectors, and then each of those vectors can be given a codeword that points to their closest centroid, creating the possibility of recovering entire pieces of the matrix from single codebook lookups, effectively storing a set of numbers into a single value, and greatly increasing compression levels. This is known as Vector Quantization, and the advantages it offers has been attracting increasing interest. "Vector Quantization" typically refers to splitting the matrices into column vectors, but these vectors can be further split into sub-vectors in a practice known as Product Quantization, which generalizes both vector and scalar quantization at its extremes. The idea is that the assembly of centroid vectors returned from the codebook using the relatively small structure of stored codewords will faithfully recreate the original, larger matrix. We will see that this has indeed proven to be a very powerful model compression technique.

Compensating for the Effects of Quantization

It makes sense that we cannot simply round all of the weights in a neural network to various resolutions and expect that things still work properly, so we must come up with a plan for how to compensate for the perturbations caused by the quantization process. As we learned above, it is possible to train or fine-tune models under simulated quantization in order to drastically increase the amount of quantization that can be performed without affecting performance in a technique called Quantization-Aware Training (QAT), which also allows for learning the quantization parameters during training. However, performing QAT requires having the hardware and data necessary to train the model, which is often not possible, particularly for very large models like today's LLMs. To address this issue, Post-Training Quantization (PTQ) techniques aim to avoid training and require only a small amount of unlabeled data to calibrate the quantization function, and Zero-Shot Quantization (ZSQ) explores the ideal "data-free" scenario which requires no data for calibration.

We will see each these techniques highlighted in more detail as we journey through the literature, so let us now board our temporal tour bus and travel back to the end of the last century, when researchers were being similarly tantalized by the power of neural networks which exceeded their hardware limitations, and first started to consider how we might hope to deploy these complex models on mobile hardware.

The History of Neural Network Quantization

Early Work in Neural Network Quantization

In the family of model compression techniques, network quantization is an only slightly younger sibling to pruning, with roots also tracing back to the formative years of backprop-trained neural networks in the late 1980s. This era of advancing computational hardware felt a resurgence of interest in neural network research, but practical use was nonetheless restricted as the complexity of problems still had to be severely limited due to hardware constraints, effectively precluding the use cases for which neural networks are best suited. While researchers had implicitly dealt with considerations surrounding numeric precision in neural networks for decades, this increasing sense of computational confinement inspired a newfound focus on reducing numeric precision for optimization, producing an impressive spread of investigations around 1990.

In 1989, Baker & Hammerstrom were the first to systematically study the impact of reduced numeric precision on network performance with the direct intention of enabling hardware optimization. Their work "Characterization of Artificial Neural Network Algorithms" was an early example of successfully training networks with backpropagation using reduced precision computation, challenging the conventional wisdom that 32-bit floating point operations were necessary for preserving network performance. Hollis et al. 1990 further studied the impact of precision constraints on backprop network training, and similarly found a sharp drop-off in learning capability at around 12 bits of precision. A year later in 1990, Dan Hammerstrom built on this previous work and investigated the design of new hardware units explicitly optimized for fixed precision calculations in neural networks, demonstrating that significant gains in efficiency could be obtained with tolerable drops in performance using 16-bit or even 8-bit precision, laying the foundation for future work in quantization and hardware optimization for neural networks.

As an interesting fact, investigations into exploiting lower bit-widths and special hardware for optimizing neural networks were being made even before backprop became the uncontested champion of neural network learning algorithms. In a formative work from 1992, Hoehfeld and Fahlman investigated the effects of limited numerical precision on training networks with the Cascade-Correlation algorithm (Fahlman & Lebiere, 1991), demonstrating that this learning algorithm was similarly receptive to operating at fixed precision. As a component of their success, the authors outline techniques for dynamic rescaling and probabilistic rounding that enable convergence at much lower precision (6-bit in their case) which are applicable to any gradient-based learning algorithm.

This foundational period in the exploration of network quantization illuminated the path for discovering the sophisticated techniques and hardware-specific optimizations that populate today's world of lumbering giants. By demonstrating the feasibility and benefits of reduced precision computation, these early works expanded the possibilities of neural network applications, providing a powerful method for developing more efficient and scalable AI systems. Today, as we stand on the brink of ubiquitous AI integration across diverse platforms, the legacy of these pioneering efforts is more relevant than ever. They not only showcased the potential of model compression and efficient computation through quantization, but also inspired a continuous quest for innovation in neural network design and optimization.

Quantization in the Post-AlexNet Era

In 2012, the authors of AlexNet capitalized on a serendipitous confluence of major developments in data availability and computational hardware to eclipse the performance of previous state-of-the-art approaches in the ImageNet Large-Scale Visual Recognition Challenge (ILSVRC). Two major elements helped to make this historic success possible: 1) the efforts of Fei-Fei Li and her team at Princeton, who provided the world's first large-scale curated image dataset, and 2) a fortuitous coincidence that the well-funded advancements in Graphic Processing Unit (GPU) technology, which were being driven by a healthy stream of gaming industry revenue, happened to produce hardware that offers the same type of parallelized computation needed to accelerate the matrix operations in deep learning.

Given these auspicious circumstances, Alex Krizhevsky and his team trained a sizeable Convolutional Neural Network (CNN) of 62.3 million parameters and blew past the competitors with a >10% lead in accuracy over the runner up, marking a watershed PR moment for neural network research, and kicking off an enduring period of intense interest and funding that is often referred to as the "deep learning revolution." However, the rejuvenated neural nets were quickly met by their old foe: hardware limitations. Despite the profound benefits of GPU-accelerated training, the authors of AlexNet conceded that hardware constraints imposed a limiting factor on the success of their approach, and that the results would likely improve with better hardware. The research community was quick to recognize the unaddressed potential of model compression to address these limitations, and rose to action. The revelations made during this CNN-focused period about the varying sensitivity levels among different types of network components would provide a strong base for the future investigations into transformers.

In fact, the echoing desires to deploy neural networks at the edge were already being heard before AlexNet shook the world. Vanhoucke et al.'s seminal 2011 work explored the acceleration of neural nets on x86 CPUs. Written at a time when the AI community was at a crossroads — debating whether to invest in GPUs or to extract more performance from traditional CPUs — their paper offered a pivotal guide on optimizing neural network operations on Intel and AMD CPUs. Predating the era of GPU dominance ushered in by AlexNet, Vanhoucke et al. showcased the untapped potential of CPUs through meticulous optimizations, including the adoption of fixed-point and integer arithmetic complemented by SIMD instructions and memory alignment techniques. Using these optimizations, the authors achieved significant performance gains, and laid the groundwork for upcoming research into the efficient training and deployment of neural networks on CPU hardware.

After the success of AlexNet, CNNs became the new soil in which a rapid-growing crop of quantization research would grow. Researchers grappled with the nuances of quantizing different types of network layers, with their varying levels of sensitivity and advantages to be offered. For instance, most of the FLOPs in CNNs occur in the convolutional layers, so quantizing them offers the best gains in speed; however, these layers also house the parameters most crucial to feature extraction, rendering them particularly sensitive to alteration. Fully-connected layers, on the other hand, tend to be much easier to compress, but doing so is advantageous mostly in terms of storage size rather than the latency, as these layers contribute less to the overall computational graph.

In addition to the distinction between techniques providing storage-only vs. full efficiency gains, there is also a distinction in the latter group between techniques which seek to accelerate both training and inference vs. those that only seek to accelerate inference. The concept of QAT was born during this period, and while many techniques opt to use simulated quantization during training, others stuck closer to the roots of network quantization and explored the use of fixed-point or integer-only arithmetic during both training and inference to pursue end-to-end neural network development at the edge.

As two early examples of these diverse approaches to CNN compression through quantization, Denton et al.'s 2014 "Exploiting Linear Structure Within Convolutional Networks for Efficient Evaluation" method improves computational efficiency by applying matrix factorization as either a PTQ or QAT procedure in the convolutional layers, while Gong et al.'s 2014 "Compressing Deep Convolutional Networks using Vector Quantization" focuses instead on achieving storage size optimization by compressing the fully-connected layers using a variety of vector quantization methods in a PTQ setting, remarking on the distinct superiority of product quantization.

In this section, we will watch the field of quantization come into focus during the era of CNN dominance unleashed by AlexNet. In this formative period of growth, we will see QAT, mixed-precision quantization, PTQ, and extreme quantization down to 1 or 2 bits become well-defined areas of research, setting the stage for our exploration into the maturation of these techniques in today's era of large models.

Quantization-Aware Training of CNNs

It was during the post-AlexNet era that QAT truly took form as a distinct area of quantization research. In former eras, nearly all work in quantization used the training process to optimize weight discretization, since the networks in question were relatively small. Even after the AI growth spurt triggered by GPU-accelerated training, the models were still trainable using a reasonable amount of resources, and concerns about avoiding the necessity of retraining quantized networks were mostly motivated by mobile deployment and data access/privacy concerns, rather than training resources. Nonetheless, the value of PTQ was becoming clear during this era, and the distinction between the two fields materialized. Given the reasonable training costs, the bulk of quantization research in the CNN era stuck to the roots of QAT-based approaches. In this section, we review the development of QAT approaches during the CNN era.

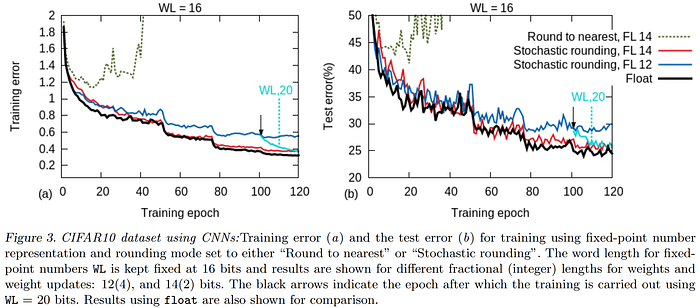
We start in late 2014, when Courbariaux et al. observed that "multipliers are the most space and power-hungry arithmetic operators of the digital implementation of deep neural networks," and investigated specifically reducing the precision of these operations for efficiency gains, since their cost scales quadratically in relation to bit width, whereas the costs of the other operators in the multiplier-accumulator (MAC) operations (the adder and accumulator) only scale linearly, and are therefore comparably inexpensive. Notably, their study showed that "the use of half precision floating point format has little to no impact on the training of neural networks." Further, the authors found that "very low precision is sufficient not just for running trained networks but also for training them," although at this point in time, "very low precision" is referring to 10-bit multiplications, an emblem of how rapidly this field has shifted bits, as we will see.

In 2015, Gupta et al. from IBM published "Deep Learning with Limited Numerical Precision," introducing a pioneering approach to training deep neural networks in 16-bit fixed-point arithmetic using stochastic rounding — where the probability of rounding a number to either of its nearest quantization points is proportional to their proximity. This rounding method outperforms the round-to-nearest approach by introducing noise which drives the expected value (bias) of quantization error to zero. Unlike conventional QAT methods that often rely on full-precision floating-point operations during training, Gupta et al.'s strategy involves executing all training computations in lower precision. The use of fixed point arithmetic allows using faster and more power and space-efficient compute units, and the authors explore hardware co-design by demonstrating a novel energy-efficient hardware accelerator. Importantly, the use of stochastic rounding ensures that even small gradient values contribute to the training process, thereby diminishing the reliance on gradient approximation methods like the Straight-Through Estimator (STE).

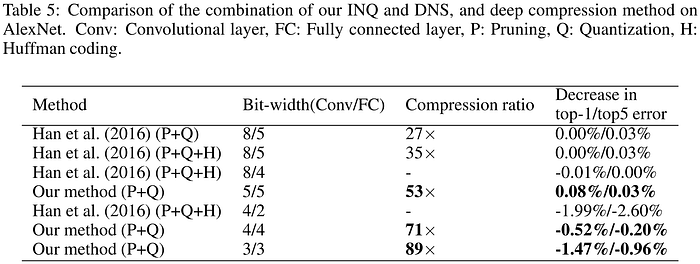
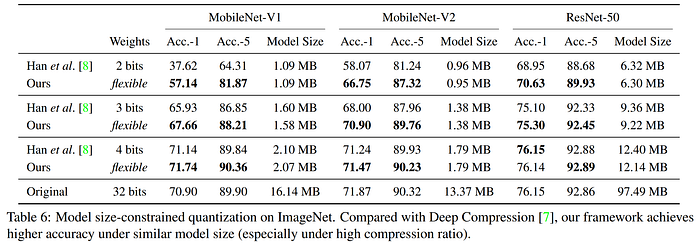
Han et al.'s 2015 "Deep Compression" is a foundational dictionary-based (i.e. codebook) method for achieving extraordinary levels of compression in neural networks without sacrificing performance using a hybrid quantization and pruning approach. Motivated to bring the breakthroughs in computer vision into mobile applications, the authors experimented on the workhorse CNNs of the day, achieving compression rates of 35x and 49x on AlexNet and VGG-16 respectively, with no loss in accuracy, by using a three-stage pipeline which sequentially prunes, quantizes, and finally applies Huffman coding (a form of lossless data compression) to the network weights. First, the unimportant weights are identified and pruned from the model using the seminal unstructured approach of Han et al.'s prior 2015 work "Learning both Weights and Connections for Efficient Neural Networks" to achieve between 9x and 13x compression with no increase in error. Second, the remaining weights are quantized from 32 down to 5 bits, followed by a round of retraining to recover performance, then the approach finishes with Huffman coding of the quantized weights for an additional 20–30% reduction in storage size.

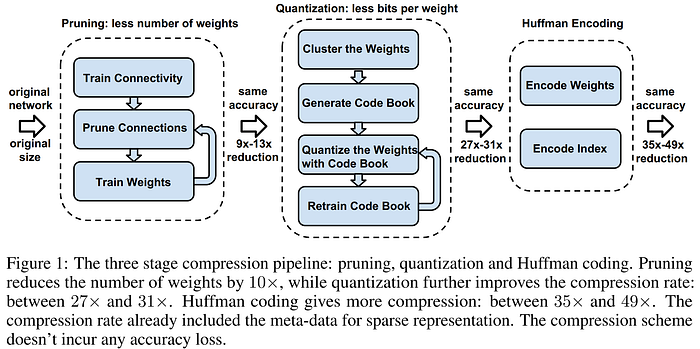
The results from "Deep Compression" are staggering, with the method compressing CNNs to less than 1/35 their original size while demonstrating equal or superior accuracy compared with their baseline references. However, it is important to remember that both the AlexNet and VGG architectures studied are intentionally overparameterized to maximize performance, and they both have contain parameter-dense yet relatively insensitive fully-connected layers and the end which can be compressed heavily. While the method is primarily focused on enhancing the storage footprint of the model, the authors remark that smaller storage also means accelerated operation, as there are less weights to store and fetch, and therefore reduced memory bandwidth requirements, particularly when the model size is reduced enough to be stored on-chip in the Static Random Access Memory (SRAM) rather than being bounced back and forth between Dynamic RAM (DRAM) and SRAM. Further, the authors introduce the concept of the Efficient Inference Engine (EIE), a hardware accelerator designed to leverage the sparsity resulting from pruning, which would be the subject of their forthcoming publication.

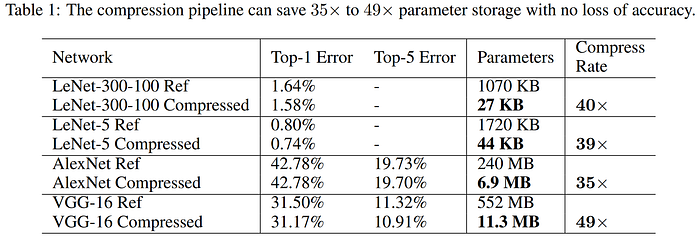
In early 2017, the Incremental Network Quantization (INQ) approach from Zhou et al. surpassed the levels of compression seen in Deep Compression. The authors also use a combination of pruning and quantization, but no Huffman coding, to achieve 53x compression on AlexNet with no loss in top-1 accuracy, and a whopping 89x compression with only minimal loss (<1.5%). Their strategy incrementally quantizes portions of the network weights, retrains the remaining full-precision weights to compensate of the induced error, and iterates until all weights are quantized. The weights are constrained be either zero or powers of 2 (think negative powers). As the authors explain, the advantage of this strategy "is that the original floating-point multiplication operations can be replaced by cheaper binary bit shift operations on dedicated hardware like FPGA." To do this, they employ a variable-length encoding, which uses one bit to indicate a zero value, and the remaining bits together indicate the codeword that indexes the possible quantized values for a given bit width and scaling factor, the latter of which they set to be the maximum absolute layer-wise weight magnitude. Their approach slightly exceeds baseline FP32 AlexNet performance with 5-bit precision, and shows comparable accuracy down to 3-bits, as seen in the chart below. Code for INQ is available on GitHub.

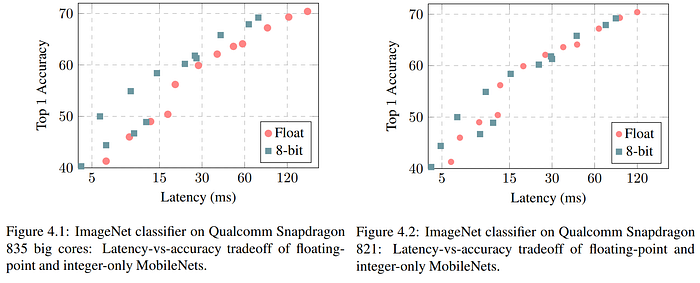
In late 2017, Jacob et al. from Google focused on enabling efficient integer-only inference at the edge on mobile device CPUs. The authors state that using intentionally overparameterized models like AlexNet and VGG to benchmark model compression techniques creates an easy target, so they opt instead to test their approach using MobileNets. Since these compact models are already designed to maximize parameter efficiency, there is less "dead weight" to be easily compressed, and their parameters are more sensitive to perturbation. Considered the formative work in QAT, Jacob et al.'s approach quantizes both weights and activations to 8 bit integers, and the biases (which require more precision) to 32 bit integers. Their method uses floating-point arithmetic during training, serving as an early example of using simulated quantization for QAT. The authors avoid a quantization scheme requiring look-up tables because these tend to be less performant than pure arithmetic on SIMD hardware, and opt instead for an affine transformation of the weights to the integer space. To complement their QAT method, the authors co-design a framework for converting and running the resulting trained model on integer-only hardware, and go a step further than many previous works by proving their efficiency gains on actual edge hardware.

So far, the techniques we've seen quantize the layers of the model to a uniform level of precision, which is the optimal condition for hardware acceleration, particularly at the edge on low-power hardware. However, as we learned in our previous exploration into pruning, some network layers are less sensitive to alteration than others, and can therefore be compressed more aggressively without affecting performance. Thus, mixed-precision quantization approaches use varying levels of compression on network components (typically at layer-wise granularity) based on their sensitivity to achieve even smaller memory footprints and reduce the data transfer and power costs of operating models at the edge. In the next section, we will see the familiar themes of sensitivity analysis inform the variable assignment of numeric precision across neural network components to maximize model compression through quantization.

The Rise of Mixed-Precision Quantization

To account for the varying levels of sensitivity between network layers to the perturbations caused by quantization, mixed-precision quantization, which involves tailoring the level of precision for individual network components based on their sensitivity, has become a popular approach for maximizing the levels of compression possible through quantization in deep networks. The challenge arises from the vast search space of mixed-precision settings, which is exponential with the number network layers. Moreover, for methods aiming to find the optimal sequence for layer-wise quantization and fine-tuning, the complexity becomes combinatorial. Thus, researchers have proposed various effective algorithms to automate the search and selection of optimal mixed-precision settings for deep networks, circumventing the infeasibility of brute-force exploration. As we will see, researchers have employed neural architecture search (NAS), reinforcement learning (RL), second-order Hessian information, as well as other types of solvers to address this problem, yielding impressive results, and establishing new levels of efficiency gains obtainable via quantization.

In late 2018, Wu et al. published the "Mixed Precision Quantization of ConvNets via Differentiable Neural Architecture Search" (DNAS) method for solving the mixed-precision problem. Their approach creates a set of network architecture parameters θ, which define subnets within a fully differentiable super net which contains all possible precision settings for every layer. The θ parameters control the probability of sampling each edge in this graph of subnets, and can be directly optimized through gradient descent. Using this technique, the authors create models bearing extreme compression in the weights (all the way down to 1 bit in some layers) which are able to beat the full-precision baselines. The DNAS method produces ResNet models which perform on par with their full-precision counterparts with up to 21.1x smaller footprints and 103.9x lower computational costs. The authors mention that their method is a general architecture search framework which is extensible to other network parameterizations, but leave this for future work.

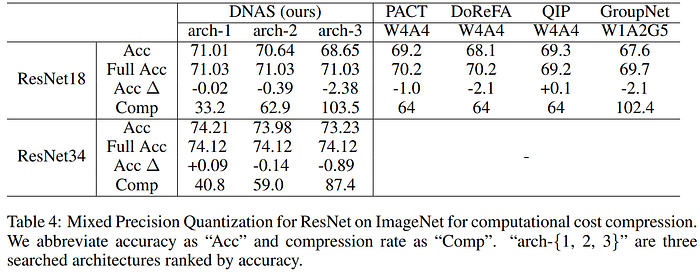
Wang et al.'s 2018 "HAQ: Hardware-Aware Automated Quantization with Mixed Precision" eschewed the use of proxy metrics for computational efficiency (e.g. FLOPs) and opted instead to use signals from a hardware simulators to feed a reinforcement learning (RL) algorithm to automate the search for optimal mixed-precision settings. While their approach pushes the limits of intelligent model compression, it suffers from weaknesses related to the complexity, computational expense, and lack of generalization that comes with training an RL policy to predict the correct mixed-precision setting for a given network architecture and hardware device.

In 2019, the Hessian AWare Quantization (HAWQ) paper addressed two significant challenges in mixed-precision quantization: the exponential search space for determining the optimal level of precision for each network layer, and the factorial complexity of determining the optimal sequence of QAT across those layers, which make brute force search of these values untenable in deep networks. The authors demonstrate that the top eigenvalues from the second-order Hessian information can provide a sensitivity analysis to inform both the correct levels of quantization and the optimal order of fine-tuning across the network layers. This is reminiscent of pruning approaches that are based on LeCun et al.'s 1989 Optimal Brain Damage, where Hessian information is used as a measure of saliency (i.e. sensitivity) of network components, with larger values indicating that the pruning or quantization of a given network component will have a greater effect on performance. HAWQ was able to exceed the performance of DNAS with 2bit weights and 4bit activations, reaching a higher overall compression as a result.

Seven months after HAWQ in 2019, Dong et al. followed up with HAWQ-V2 to address three major limitations they identified in their previous work: 1) only using the top eigenvalues for sensitivity analysis, ignoring the rest of the Hessian spectrum, 2) only determining relative layer-wise sensitivity measurements, necessitating manual precision assignments, and 3) not considering mixed-precision quantization for activations. Addressing the first issue, they find that taking the average over all Hessian eigenvalues is a superior measure of layer-wise sensitivity. For the second, the authors propose to use a Pareto frontier-based method for automatically selecting exact layer-wise bit precisions. To address the third weakness, the authors "extend the Hessian analysis to mixed-precision activation quantization." With these adjustments, HAWQ-V2 set a new state-of-the-art benchmark in CNN quantization.

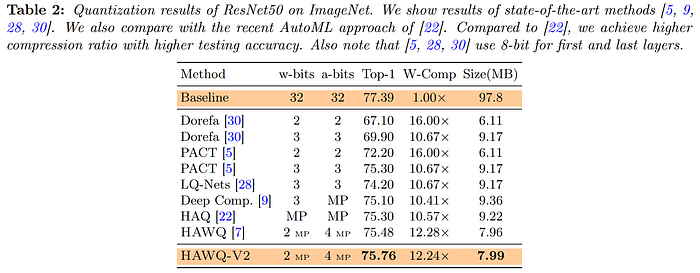
A year later in late 2020, the HAWQ authors published a third iteration, HAWQ-V3. This work improved on the previous approaches by ensuring integer-only arithmetic in every network operation, including the batch norm layers and residual connections, which were previously kept in float32 to maintain accuracy, thereby preventing deployment in the types of integer-only hardware common in edge devices. To determine layer-wise bit precision, HAWQ-V3 uses a "novel hardware-aware mixed-precision quantization formulation that uses an Integer Linear Programming (ILP) problem," which "balances the trade-off between model perturbation and constraints, e.g., memory footprint and latency." Their approach produces a model that performs integer-only inference in 8bits which exceeds the performance of the strongest available full-precision baseline, demonstrating "free lunch" compression, and maintains high accuracy at precisions down to 4bit.

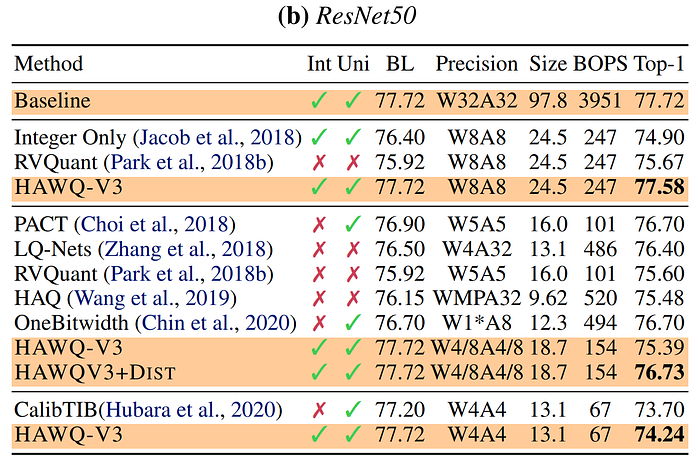
The techniques covered in this section show the power of adjusting the layer-wise precision assignments based on sensitivity analysis, quantizing insensitive layers more aggressively, and allowing higher precision to preserve representation power in the sensitive layers. However, it is important to note that mixed-precision quantization schemes can be more challenging to implement on edge devices, where they may not operate as efficiently. Thus, it is reassuring to see strong fixed precision benchmarks in the HAWQ-V3 results above. In the next section, we will discuss techniques which seek to perform quantization on trained, full-precision CNNs without the need to retrain them, a highly relevant precursor to our upcoming discussion on the quantization of LLMs, where retraining and access to training data are often impossible.

Post-Training Quantization of CNNs

The astute reader will notice that the majority of works in this section on quantization during the CNN era belong to the QAT category, since the models studied during this period were easy enough to fine-tune in a quantized setting. However, even before the imminent explosion in neural network sizes, researchers were already keen on the practical advantages of PTQ, which promised to liberate those developing quantized models from the need to gain access to the original training data (which may be impossible in many cases), as well as save the time and resources required for retraining. Thus, a timely wave of interest in PTQ research caught steam around 2019, laying a welcome groundwork for the focus on large language models yet to come.

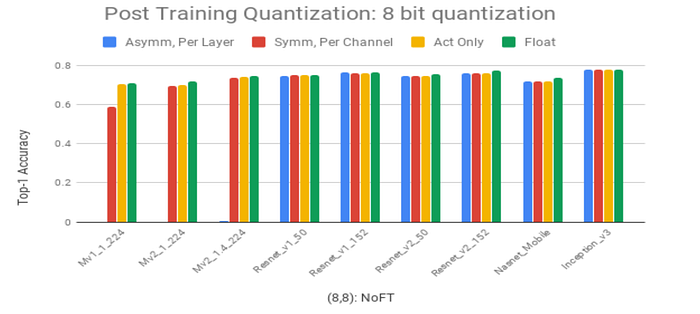
Krishnamoorthi led this charge in mid-2018 with a seminal white paper on CNN quantization. Their approach uses channel-wise asymmetric uniform quantization of weights and layer-wise quantization of activations to a fixed precision of 8 bits while maintaining accuracy within 2% of baseline. The author observes that quantizing only the weights of a network to 8-bit can be an easy way of compressing storage size, but in order to enable efficient inference, activations must also be quantized, which requires using calibration data to calculate the dynamic ranges of activations throughout the network layers to discover the appropriate layer-wise quantization parameters. In the chart below, the author provides a comparison of the effects of per-layer and per-channel weight quantization schemes on various CNNs. Notice that the larger, overparameterized CNNs towards the right are much more receptive to the lower granularity of per-layer quantization parameters than the efficiency-minded MobileNets (left).

In October 2018, Banner et al.'s "Post training 4-bit quantization of convolutional networks for rapid-deployment" sought to expand the usability of PTQ to below 8bits of precision. Their approach efficiently achieves 4-bit data-free mixed-precision PTQ with tolerable performance degradation. To do this, the authors exploit the knowledge that neural network distributions tend to be bell-shaped around a mean in order to tune their quantization scheme in a way which minimizes the mean-squared quantization error at the tensor level, thereby avoiding the need for retraining. To allow for better knowledge transfer into the quantized space, the authors 1) use their proposed analytical clipping for integer quantization (ACIQ) technique to clamp activation tensor outliers according to an optimal saturation point which reduces rounding error in the more densely populated region of the spectrum, 2) determine optimal per-channel bit allocations analytically, finding that the optimal quantization step size for a given channel "is proportional to the 2/3-power of its range," and 3) propose a simple bias-correction method to compensate for the biases introduced into the weights after quantization by incorporating the expected changes in their channel-wise mean and variance into the quantization parameters.

The ACIQ approach requires statistical analysis of network activations on a small calibration set, so while it does not require access to the training data, it is essential to ensure that the calibration set is representative of the distributions that will be encountered during runtime, otherwise there is risk of overfitting quantization parameters to the wrong distribution. Also, note that the use of channel-wise bit width creates a lot of concerns for practical application, as both hardware and software must be catered to support mixed-precision at the channel level, or otherwise running the quantized network may be inefficient or impossible. Nonetheless, the formulation of a closed-form analytical solution to directly calculate the optimal bit-widths for network components marks an important milestone in quantization research. Further, their closed-form PTQ solution for bias correction parameters, as well as the efficient absorption of these parameters into existing calculations, marks another significant contribution. Code for Banner et al.'s approach is available on GitHub.

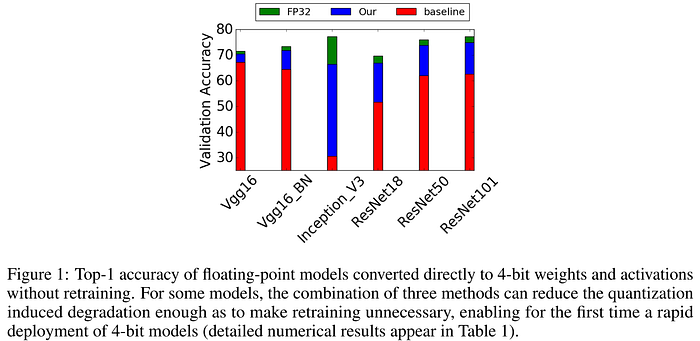
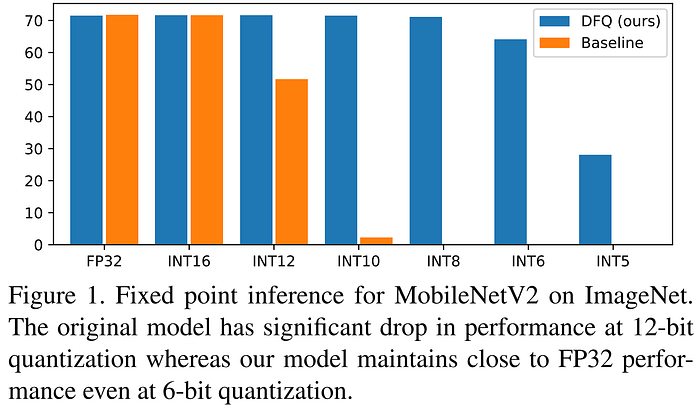
Nagel et al.'s 2019 "Data-Free Quantization Through Weight Equalization and Bias Correction" (DFQ) introduced a groundbreaking approach to data-free PTQ, enabling deep networks to be efficiently quantized down to 8 bits without the need for calibration data, fine-tuning, or hyperparameter tuning. The authors adapt the weights through scaling to make them "more amenable to quantization," propose a method for correcting the biases introduced by quantization, and mention that their approach could be employed as a complementary pre-processing step to QAT. Unlike the Krishnamoorthi and Banner et al. approaches above, which require storing quantization parameters for each channel, DFQ requires storing only a single scale and offset value for each layer's weight tensor by determining the values that maximize the per-channel precision across that layer. DFQ exploits the scale equivariance of the ReLU activation function and keeps the overall math equivalent by absorbing the scaling and induced bias into the next layer. The authors demonstrate that the need for calibration data to quantize activations can be avoided by using the batch normalization statistics preserved in the model from its training to estimate the layer-wise expected quantization error, and compensate for the bias introduced into layer activations through quantization by subtracting this expected error from the layer bias parameters. Although the authors do not explicitly use the term, DFQ can be seen as a formative work in zero-shot quantization (ZSQ), as it is a PTQ approach which requires no calibration data.

Choukroun et al.'s 2019 OMSE method finds the kernel-wise quantization parameters which minimize the mean squared error (MSE) between the quantized and original weight/activation tensors, marking the first PTQ approach to achieve 4-bit quantization with minimal loss in accuracy (3% degradation on top-1 ImageNet classification). The authors opt to use symmetrical uniform quantization for highest efficiency, saving the additional calculations introduced by using offsets. Since the relationship between quantization-induced MSE and scaling factor for a given kernel is non-convex, the authors use a line search method to discover the optimum values. To circumvent the need for using mixed-precision to preserve representation power in the sensitive network layers, the authors propose to represent these "key" layers using multiple low-precision tensors, but they warn that the complexity of this approach necessitates using it only for small tensors, which in the case of CNNs works out fine, since the most sensitive components are the convolutional kernels, but it would not scale well for architectures with large salient components.

In early 2020, the authors of the HAWQ papers published ZeroQ: a data-free PTQ approach which beat the previous state-of-the-art ZSQ benchmark set by DFQ. Their approach achieves mixed-precision quantization through a novel Pareto frontier based method which automatically determines the optimal mixed-precision setting with no manual searching. Rather than requiring access to training or calibration data, ZeroQ generates a synthetic dataset tailored to match the statistics in the batch normalization layers, called "distilled data," and then uses the activations generated by this data to calibrate quantization parameters and to perform layer-wise sensitivity analysis. These sensitivity values feed the Pareto frontier selection process, which finds the optimal setting for a given model size or desired level of accuracy. The authors call out the fact that most work in PTQ typically only benchmarks image classification accuracy without considering more complex tasks, so they also prove their method preserves performance on the more challenging object detection task. ZeroQ is open-sourced and extremely compute efficient, offering a low barrier for entry on network quantization.

Later in 2020, the authors of AdaRound pointed out the fact that the round-to-nearest approach had dominated previous work in quantization, despite being a suboptimal rounding scheme. Instead, they proposed a framework to analyze the effect of rounding which considers characteristics of both input data and task loss, and formulate rounding as a per-layer Quadratic Unconstrained Binary Optimization (QUBO) problem. They approximate change in task loss with respect to weight perturbations using a second-order Taylor series expansion, in the familiar way used by other works using Hessian information to measure sensitivity, starting with Optimal Brain Damage (OBD) in 1989. Like Optimal Brain Surgeon (OBS), they extend their method to benefit from deeper theoretical analysis of the off-diagonal Hessian values. They equate the naïve round-to-nearest approach to considering only the diagonal of the Hessian, wherein perturbations are assumed to have no codependence in their contribution to the task loss, and therefore only the reduction of their individual magnitudes matters (i.e. round-to-nearest). However, the effects of weight perturbations are interrelated, and the off-diagonal information is therefore important, as it can signal when combinations of perturbations are actually beneficial to the loss. AdaRound requires only a small amount of unlabeled data, and set a new state-of-the-art in PTQ for CNNs, compressing ResNet models to 4bit while staying within 1% of their baseline performance.

To show their point quite vividly, the AdaRound authors generated a set of 100 random perturbations for the first layer of ResNet using the stochastic rounding method from Gupta et al., 2015 (above), and compared these to a round-to-nearest perturbation. Of the 100 sampled layer perturbations, 48 had better performance than rounding to nearest, with some providing more than 10% accuracy improvements. This demonstrates there are many better solutions in the quantized space, and provides a clear signal that there should be ways of targeting them to increase the accuracy of PTQ.

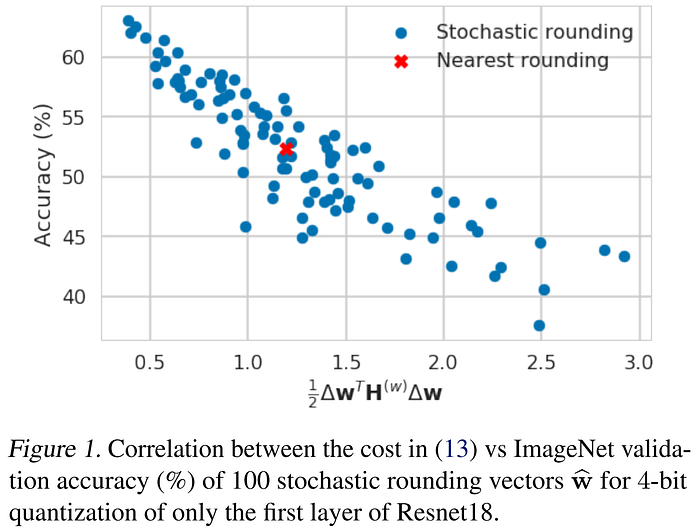
In the chart above, we can see a clear correlation between the second-order Taylor series term and the drop in accuracy after rounding, indicating that this is a good proxy for optimizing task loss due to quantization. Even ignoring the cross-layer interactions among network weights, however, the Hessian is still prohibitively costly to compute for large network layers. The results below show that a W4A8 configuration of AdaRound can come close to the performance of the FP32 baseline and W8A8 DFQ. However, in this comparison it is important to note that AdaRound is not a data-free or "zero-shot" approach like DFQ is.

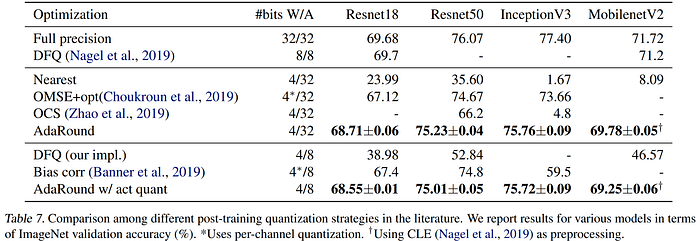
Only a couple months after AdaRound in mid-2020, AdaQuant took things a step further to introduce a new PTQ method which could quantize both the weights and activations to 4-bit while retaining performance, with less than 1% ImageNet top-1 accuracy degradation using ResNet50. The authors circumvent the limitations of AdaRound by using a small calibration set to minimize layer-wise quantization MSE in both the weights and activations one layer at a time, using channel-wise granularity. They note that the quantization process introduces an inherent bias and variance into the batch norm statistics, and propose to recover performance degradation by re-estimating these statistics in their proposed Batch Normalization Tuning (BNT) approach. The authors offer both a mixed and fixed precision variant of AdaQuant, and the code is available on GitHub.

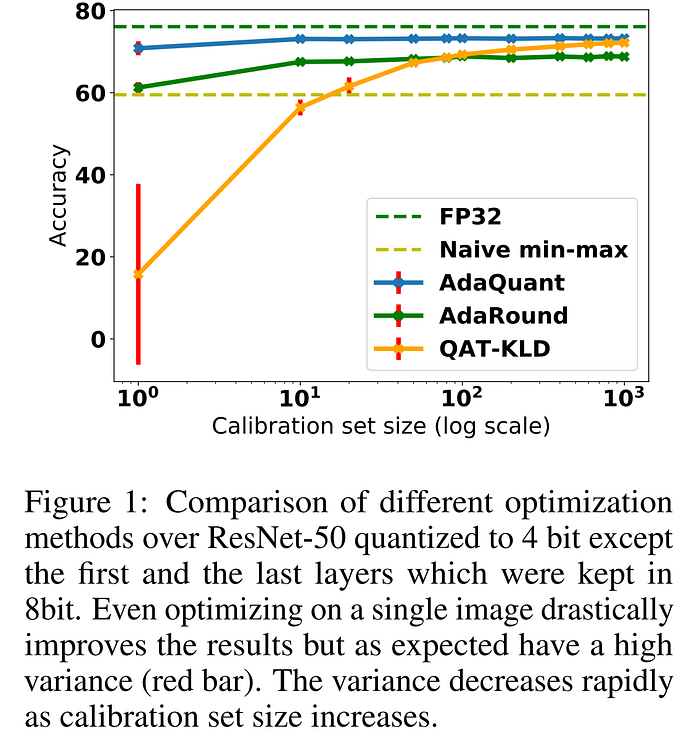
In this section, we've seen the rising focus on PTQ methods in the post-AlexNet era. While the primary motivators for PTQ during this period were typically concerns about edge deployment and data privacy, the work covered here provided an important foundation for the upcoming reliance on PTQ approaches that would arise with the exploding model sizes in the years to come. Before we part ways with the CNN era, there is one more research trend which was coming into fruition during this period that we need to cover, which was also motivated by the desire to operate at the edge: the extreme quantization of neural networks down to only 1 bit (binary networks) or 2 bits (ternary networks).

Extreme Quantization: Binary and Ternary Networks

Extreme quantization refers to compression at ≤2 bits, meaning either ternary (2-bit), or binary (1-bit). The ability to effectively compress models down to these levels of precision comes with obvious benefits, as the models become 16–32 times smaller than their FP32 counterparts, allowing for deployment on smaller edge devices using far less power consumption, and saving valuable on-chip real estate for optimizing computation speed. Unsurprisingly, reducing the precision of neural networks this low comes with equally extreme challenges, due to the loss of representational power. However, the costly multiply-accumulate (MAC) operations in network computation can be entirely replaced in both binary and ternary networks by far more energy-efficient addition/subtraction and bit shift operations, making the potential gains radical, and galvanizing researchers to tackle the challenges involved. In this section, we observe the compelling results which arose from the developing field of extreme network quantization during the CNN era, and discover why it has since become such a highly magnetic and frequently cited field: the extraordinary gains in efficiency offered by low-bit networks are hard to ignore. Moreover, we will see that binary nets can be ensembled to use an equivalent number of bits as a fixed-point network to exceed its performance while maintaining all the benefits of binary arithmetic. First, let us rewind to 2014, so that we can build our understanding of low-precision networks bit-by-bit.

As a pioneering work in extreme quantization, the 2014 study by Hwang & Sung from Seoul National University titled "Fixed-Point Feedforward Deep Neural Network Design Using Weights +1, 0, and -1" is a QAT approach which obtains ternary (2-bit) weights and 3-bit activation signal with negligible performance loss. In contrast, the authors observe that the biases must be allotted a higher precision of 8 bits in order to preserve performance. The quantization thresholds are initially chosen to minimize MSE between the original and quantized tensors, and then an exhaustive search is performed in each layer one-by-one in order to tune these initial proposals to their optimal values which minimize the network output error. Finally, the quantized weights are fine-tuned using a fixed-point backpropagation scheme that is modified to handle the quantization. While the authors set a foundational precedent in the field of extreme neural network quantization, their use of exhaustive search is a testament to the smaller model sizes of the day, and more scalable solutions would become necessary for the growing models sizes in the coming years.

In 2015, Courbariaux et al. presented the "BinaryConnect" algorithm. As the name suggests, their method produces a binarized network, in which the weights are constrained to be either -1 or 1. The authors remark that noisy weights, i.e. weights that are discretized using a stochastic rounding scheme, "are quite compatible with Stochastic Gradient Descent (SGD)," as we saw earlier in Gupta et al.'s 2015 work on stochastic rounding. Like the approach of Hwang & Sung above, the authors apply the gradients from the loss generated by the quantized weights to update the full-precision weights (which are stored separately), and the quantized weights are derived from the current state of the full-precision weights for each forward pass. The authors demonstrate that both deterministic binarization (simply taking the sign of the weight) and stochastic binarization (using weight magnitude to derive probability) both work well as regularization mechanisms (similarly to dropout) in the networks studied, demonstrating slower convergence curves with lower final validation error compared with the non-regularized full-precision baseline. While these results are very exciting, it is important to consider the fact that neither the CIFAR-10 dataset nor the CNN being trained in their study are particularly complex by today's standards, so it is not clear at this point if these results would hold up using deeper networks or more challenging tasks. The code for BinaryConnect is available on GitHub.

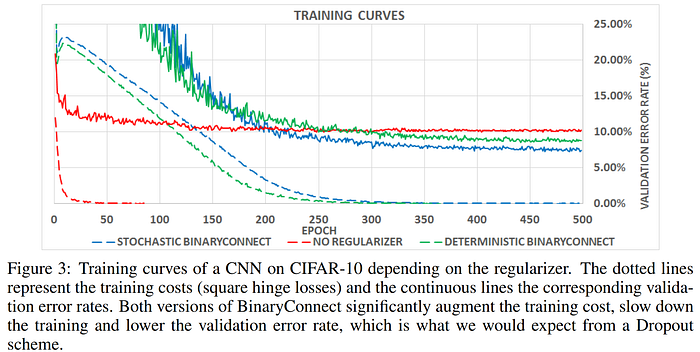
Later in 2015, Lin et al.'s "Neural Networks with Few Multiplications" extended the work and codebase of BinaryConnect in a fork of the original repo to include a ternary variant of their stochastic binarization approach called "TernaryConnect," and also introduced a quantized back propagation (QBP) scheme, where network activations are quantized to integer powers of two so that the expensive multiplication operations in the backwards passes can be replaced by efficient bit shift operations, further increasing training efficiency, and ticking another checkbox on the list of network operations which can be binarized.

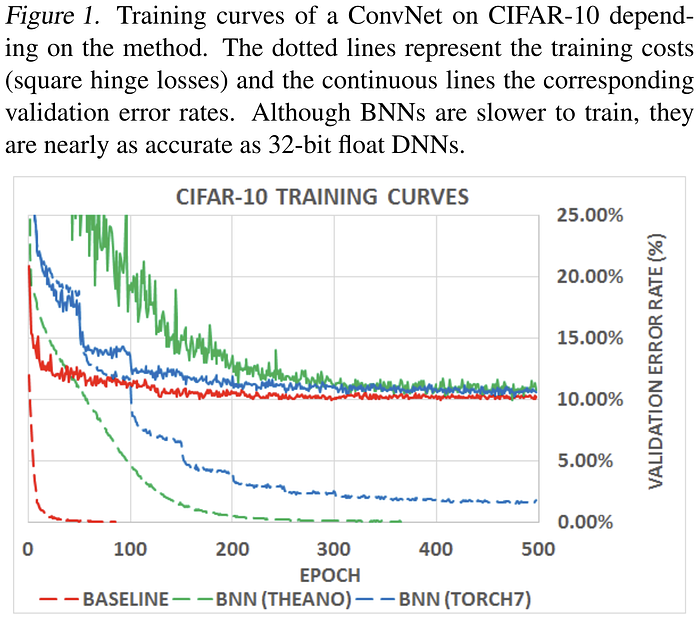
In 2016, Courbariaux and his colleagues built on this work a third time to enable binarization of activations during training. In their seminal paper "Binarized Neural Networks: Training Neural Networks with Weights and Activations Constrained to +1 or −1" (BNN, or also often referred to by the name of their first draft and GitHub repo: "BinaryNet"), the authors again compare deterministic vs. stochastic binarization, observing that while stochastic binarization is theoretically and empirically superior, the simplicity of not having to generate random bits during training makes deterministic binarization very appealing. Thus, the authors employ a best-of-both-worlds approach in which stochastic binarization is used only on the activations during training. Seeking further improvements, the authors address the costly multiplications required by batch normalization (BN) layers in neural networks, and propose a method to avoid these costly operations and maintain the binary nature of network operations using shift-based batch normalization (SBN), which approximates the effect of BN using inexpensive bit-shift (power-of-two scaling) operations instead of multiplications. In conjunction, the authors propose a shift-based AdaMax optimization algorithm to circumvent the multiplications required by the canonically employed Adam optimizer, and show that training outcomes are unaffected by the noise introduced by either of these approximations. Testing their approach once again on basic CNNs with the CIFAR-10 dataset, the authors demonstrate compelling results using binarized weights and activations to train neural networks. Code for training these Binarized Neural Networks (BNNs), complete with the customized GPU kernels, is available online.

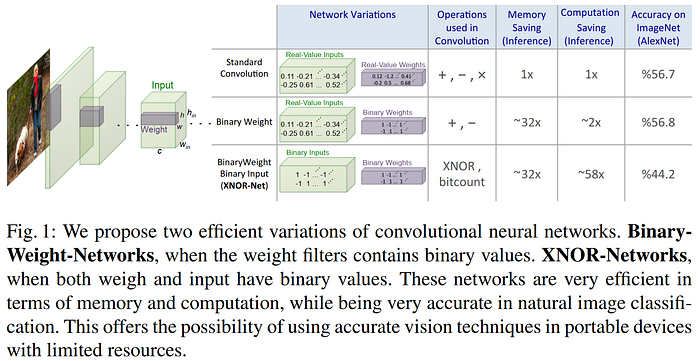
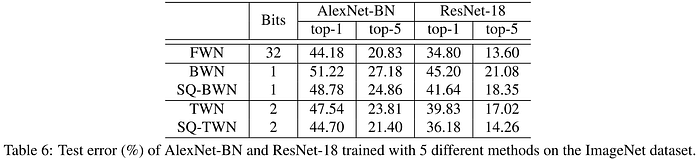
Rastegari et al.'s 2016 XNOR-Net paper was the first to test CNN binarization on the large-scale ImageNet dataset, showing that BinaryConnect and BNN (aka BinaryNet) don't work as well at these scales. The authors exceed the results of BNN by 16.3% on top-1 ImageNet accuracy by introducing a new method of weight binarization which incorporates weight scaling, and find that the optimal scaling factor for a given weight matrix is the average of its absolute values. Similar to BinaryConnect and BNN, the authors update a separate set of full-precision weights using the gradients calculated from the quantized forward passes using the STE, although they do not opt to use the shift-based approximations for BN and Adam offered in the BNN paper. The drop in performance from their Binary-Weight-Network (BWN) configuration to the XNOR-Net configuration highlights the difficulty of discretizing activation signals in more complex tasks like ImageNet, but binarizing these representations is especially ambitious. Nevertheless, the fact that the weight-only binarization can achieve the same performance as the baseline CNN looks like yet another promising opportunity for "free lunch" compression, and the fact that the XNOR-Net version can still achieve reasonable performance even with full signal binarization is compelling. The code for XNOR-Net is also available on GitHub.

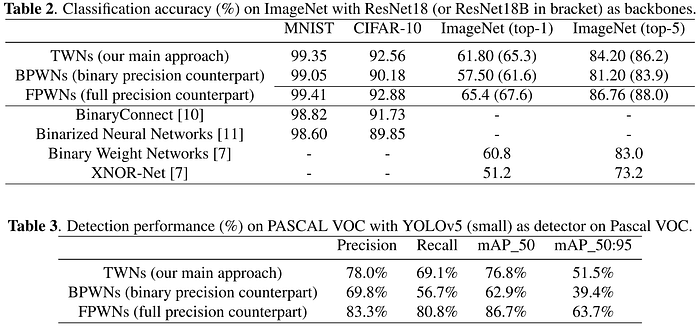
Li et al.' 2016 "Ternary Weight Networks" (TWN) is a QAT approach which trains ternary networks from scratch. Their quantization scheme seeks to minimize Euclidean distance between the quantized and raw weights using learned layer-wise scaling factors and ternarization thresholds set to 3/4 the average magnitude per weight tensor to approximate the full-precision weights as closely as possible. The authors observe that ternary networks "show better expressive capabilities than binary precision counterparts," and demonstrate this concept using the example of binary vs ternary 3x3 convolution filters, which can take on 512 and 19683 possible unique templates, respectively. Their experiments prove that this additional expressive power is beneficial on various tasks, including MNIST, CIFAR-10, ImageNet, and the Pascal VOC object detection task. In the results below, we can see that this additional expressive ability of ternary networks is particularly beneficial in the more challenging ImageNet and Pascal VOC tasks, a possible signal that the optimism we were experiencing from the very promising binarization results we saw above on less complex models and tasks may not hold up as the complexity grows.

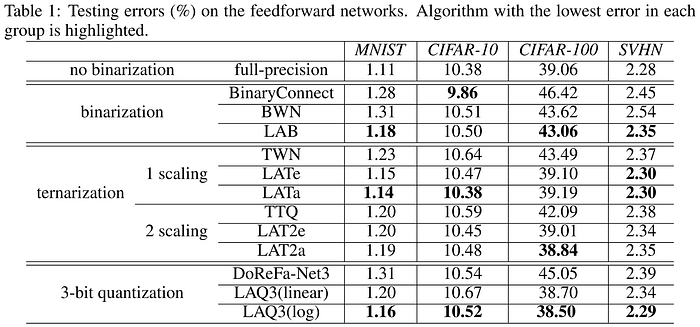
In late 2016, Hou, Yao, and Kwok published "Loss-aware Binarization of Deep Networks" (LAB), which filled an empty research lane left by previous methods which had not optimized the binarization process based on its impact on the cost function directly. To binarize the network in a way which minimizes the cost function, the authors solve a proximal Newton algorithm by using the second-order gradient information captured in the Adam optimizer to efficiently extract a diagonal Hessian approximation, rather than computing the Hessian directly. The authors show that their method is "more robust to wide and deep networks," and also extend their investigation into NLP tasks using Recurrent-Neural Networks (RNNs). Then in early 2018, Hou & Kwok extended their LAB algorithm to produce higher-precision networks in "Loss-Aware Weight Quantization of Deep Networks" (LAQ, or LAT in the ternary case), showing that the proposed method improved results further over the binarization offered by LAB.

In 2017, Dong et al. proposed the stochastic quantization algorithm: a QAT approach to extreme quantization in which only a portion of the network elements/filters (inversely proportional in size to the quantization error) are quantized during each training step, and updated separately from the full-precision weights. As training progresses, eventually all weights are quantized, and the resulting low-bit network maintains significantly better accuracy than equivalent BWN and TWN models.

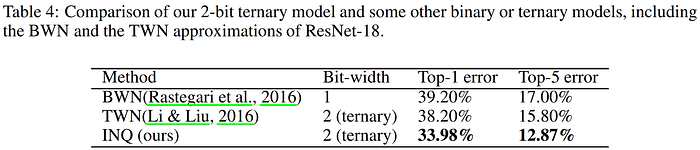
The 2017 Incremental Network Quantization (INQ) paper we saw earlier in the QAT of CNNs section, which surpassed the previous state-of-the-art in model compression set by Deep Compression in 2015, also investigated the viability of their approach in creating ternary networks. In the chart below, we can see that their approach is notably superior to TWN in ResNet-18 trained on the ImageNet classification task, reducing the error by over 4%. Looking above, we can also see that it beats the 36.18% top-1 error rate of the stochastic-quantized TWN (SQ-TWN) by over 2%.

Later in 2017 Lin et al.'s "Towards Accurate Binary Convolutional Neural Network" (ABC-Net) paper sought to overcome the lack of representational power in binary networks by combining multiple sets of binary weights or activations to more faithfully represent the high-precision values, showing that by using 3–5 weight bases and 5 binary activations, the accuracy degradation on ImageNet can be reduced to 5% from baseline. The authors point out that while this requires the use of more bits, the scheme is preferable to using higher-bit fixed-point representation because it still avoids the need for the more complex arithmetic operators as the bitwise math is still done in binary. Their work marks the first time that binary neural networks reached comparable performance on ImageNet to full precision baselines, but their solution increases baseline BNN complexity by O(k * l), where k is the number of weight bases and l is the number of activation bases used, so there is a notable loss in efficiency.

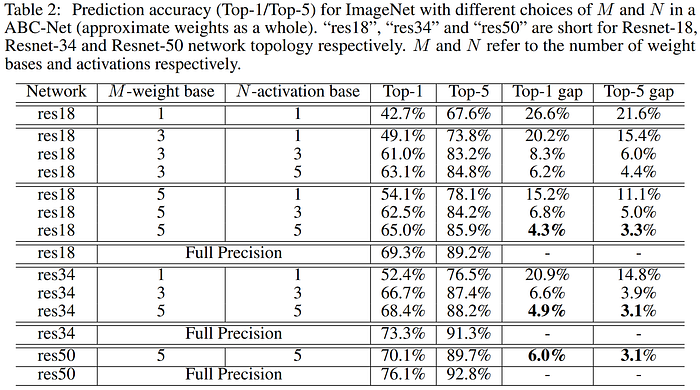
Zhu et al.'s 2018 "Binary Ensemble Neural Network: More Bits per Network, or More Networks per Bit?" (BENN) paper argued that the limitations of BNNs are not solvable through further optimization of the binarization process, since they are rooted in the lack of representational ability of the binary space. The authors aimed to reduce the prediction variance and improve the robustness to noise when using binary networks, achieving this by creating ensembles of multiple BNNs using boosting or bagging. Their experiments demonstrate that the statistical properties of the ensembled classifiers improve, and the performance improves drastically as a result. The added complexity of executing these ensembles is only O(k), more efficient than ABC-Net by a factor of l, and outperforms it significantly on ImageNet. Moreover, because the ensemble can be parallelized, the solution can have O(1) added complexity, and run just as fast as the baseline BNN.

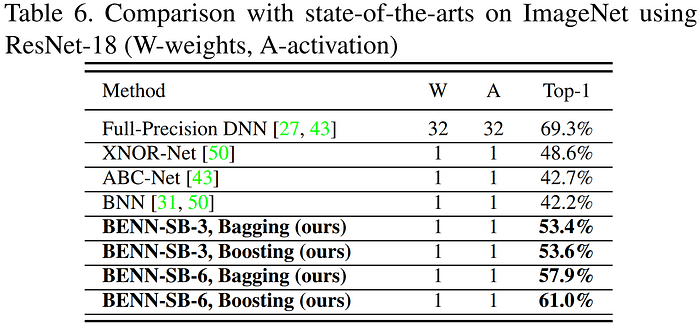
In this section, we've witnessed the explosion of interest in extreme neural network quantization following the advent of large CNNs which began after the resounding success of AlexNet in 2012. The tantalizing urge to deploy the newfound heights of modeling capabilities in this era on edge devices with low-power hardware was irresistible, as this is where many practical applications of deep learning exist. Note that most of the methods in this section train low-bit networks from scratch without quantizing pretrained weights, which is more easily facilitated in the fully quantized approaches by their extraordinary efficiency. Later, we will see that this impressive period of foliation in extreme quantization methodology would mature into a fertile bed of soil in which future breakthroughs would be made.

For now, we close our chapter on the CNN era, as now we have seen the formation of several distinct areas of quantization research flourish after the success of AlexNet brought massive influxes of talent and funding into the deep learning field. We've seen QAT approaches achieve impressive levels of compression without losing performance by fine-tuning the quantized weights, mixed-precision techniques achieve new levels of compression by incorporating sensitivity analysis into the quantization process, PTQ approaches closely match baseline performance in 8 or even 4 bits of precision with no retraining (and in the case of ZSQ, without using any calibration data), and finally, we saw the rise of extreme quantization research. Now, we shift our focus from the CNN era to the wave of research interest in NLP born from the success of the transformer architecture in 2017.

Quantization of LLMs

Now that we are familiar with the functional details and history of quantization, we can proceed in our discussion of quantizing the large language models (LLMs) of today. As we saw with pruning, the transition into the world of large models comes with diminishing hopes of employing compression techniques that require model training, such as QAT, for anyone but the largest outfits. Therefore, we will see a shift in research focus towards the more lightweight methods of PTQ, although the unique challenges of operating at large scales did not stop the ingenuity of the research community from finding ways of accessing the benefits of QAT, as we will see. In this section, we first review the quantization efforts that took place in the period between the publication of the transformer in the seminal 2017 paper "Attention is All You Need," and the dawn of LLMs marked by the monumental release of the 175B (billion parameter) GPT-3 in 2020. Then, we review the proliferation of PTQ methods in the LLM era, subsequently shift our focus into QAT approaches for LLMs, and finally close our investigation by reviewing the extreme quantization of LLMs. This section will complete our education in quantization, qualifying us to move on to the implementation guide in the next section, and begin employing neural network quantization in our own workflows.

Quantization in Early Era of Transformers

As we saw in the last section, the success of AlexNet in computer vision set off an explosion of research interest in quantizing CNNs for their efficient deployment, but investigations into the application of quantization in language models wouldn't pick up speed until years later, with the catalytic moment being the striking success of the transformer architecture. Before the explosive growth of language model sizes that began with the release of GPT-3 in 2020, there was a period of more reasonably-sized explorations in NLP using transformers, although the tendency for these models to continue gaining performance with increasingly large sizes was quickly becoming clear. Here, we review the formative period of quantization research in transformer-based language models that occurred during this formative period between the advent of transformers and the rise of multi-billion parameter transformer networks. A we will see, this new network architecture posed unique challenges to quantization, particularly at low bit widths, which researchers moved quickly to understand and overcome.

The seminal Bidirectional Encoding Representation Transformer (BERT) published by Google in late 2018 continues to be a highly influential transformer-based language model. BERT trains on a masked language modeling (MLM) objective to learn how to encode bidirectional context to produce embeddings which consider information that appears both before and after a given input token in the input sequence, resulting in representations that contain deep contextual understanding, useful for tasks like sentiment classification and question answering. While BERT uses an encoder-only variant of the transformer architecture to create these bidirectionally encoded representations, the Generative Pretrained Transformer (GPT) models of OpenAI fame, by contrast, use a decoder-only transformer architecture to perform an autoregressive modeling task on Byte-Pair Encoded (BPE) text, considering only the preceding tokens in the sequence, and iteratively predicting the upcoming tokens. The revelations made about the potential scalability of these autoregressive decoder-only transformers and their unlabeled pretraining datasets in the GPT-2 paper would ultimately inspire the release of the unprecedentedly large 175B GPT-3 behemoth in 2020, but as we will see, the research in transformer quantization would already be well underway by then.

In late 2019, Shen et al. from UC Berkeley published Q-BERT, a QAT method which expanded on the Hessian-based sensitivity analysis of HAWQ by additionally considering the variance of the Hessian spectrum, rather than only the mean, across the subsample of training data. Q-BERT uses this improved measure of sensitivity to establish a layer-wise mixed precision quantization scheme, and then quantize each layer at their respective bit-widths using a group-wise granularity in which the matrices are split into sub-units that each have their own quantization range and look-up table. Using their method, the authors achieve 13x compression in the weights, 4x smaller activation size, and 4x smaller embedding size with a maximum accuracy drop of 2.3% from the baseline BERT. Like most QAT techniques, Q-BERT uses the STE in order to approximate the gradients through the non-differentiable quantization function.

In contrast to Q-BERT's focus on maximizing compression using mixed precision, a contemporaneous work in late 2019 from Zafrir et al. at Intel, Q8BERT, focused instead on applying uniform 8-bit quantization across the model and activations, which is more advantageous from a hardware optimization perspective, as mixed precision operations tend to add overhead and are not conducive to generalized hardware acceleration. Their method performs QAT as a fine-tuning phase on pretrained BERT models to achieve 4x compression with minimal accuracy loss of 1% or less using a simulated quantization approach based on the Jacob et al. 2017 paper we saw earlier in the CNN quantization section, which again uses STE for gradient approximation. The scaling factor for the weights is calibrated using the maximum absolute weight magnitude, and the scaling factor for the activations is based on an exponential moving average that is accumulated during training.

In 2020, Fan et al. presented Quant-Noise, a QAT technique for achieving high rates of model compression by randomly quantizing just a subset of the network weights during each forward pass during training. The allows the majority of weights receive updates without the error introduced by the STE approximation, allowing their values to more accurately shift in ways that reduce the impact of the quantized subset. Over time, this leads to superior results than using QAT on all of the network weights at once. Quant-Noise investigates the use of Product Quantization (PQ), in which multiple weights are quantized together into single codewords, which allows for very high levels of compression with relatively low drops in performance. This approach takes advantage of the correlations between weights induced by the structure of the network.

In 2020, Zadeh et al. from University of Toronto published GOBO, a dictionary-based PTQ method for attention-based models which can use non-uniform quantization to compress nearly all of the FP32 weights in BERT to 3 bits without losing accuracy. The outliers are preserved in full precision to protect accuracy, and are automatically detected using a Gaussian distribution fit, while the rest of the weights are stored with 3-bit codewords which index a small set (8 in the case of 3-bit) of representative FP32 centroids. Since typical hardware cannot perform operations on 3-bit values directly (as the authors of Q-BERT also noted in their study), the GOBO authors develop a novel hardware architecture which enables the efficient acceleration of 3-bit computation to complement their quantization method. While the acceleration benefits are only fully accessible using the specialized hardware, the reduced memory footprint of the 3-bit quantized model will lead to reduced memory storage and traffic on more general hardware, and therefore will still provide some level of improvement in inference latency and energy consumption. The GOBO method was inspired by the storage of Huffman-encoded weights in a dictionary of few representative values (centroids) seen in "Deep Compression," but in contrast does not require fine-tuning, greatly improves accuracy by not quantizing weight outliers, and uses a novel "centroid selection algorithm that converges 9x faster than K-means and consistently reduces the number of required centroids by half."

Zhang et al.'s 2020 TernaryBERT combined Knowledge Distillation (inspired by TinyBERT) with ternary quantization in what they call distillation-aware ternarization, treating the ternarized model as a student model to the full-precision, equally-sized teacher. Their distillation method involves MSE minimization between teacher and student for the embedding layer, the outputs and attention scores of transformer layers, and the logits from the prediction layer with soft cross-entropy. TernaryBERT achieves comparable performance with the full-precision baseline, while being 14.9x smaller. The authors find that min-max 8-bit quantization works best for activations in BERT, since they find the distributions in BERT activations to be skewed towards negative values, particularly in the early layers. Their QAT process initializes weights from the full-precision model, and uses the STE to approximate gradients through the quantization function.

In 2020, BinaryBERT sought to bring BERT quantization to the extreme, but observed that a binary BERT model is hard to train directly due to its highly irregular loss landscape. Thus, the authors opt instead to train a half-sized ternary network, convert it into a binary network trough their proposed ternary weight splitting method, then fine-tune the result to achieve 24x compression of BERT with a minimal performance drop. They extend this concept to include adaptive splitting, where the more important layers are split and less sensitive layers are described in binary, to allow flexibility for different model size constraints. Like most QAT methods, BinaryBERT trains using the STE.

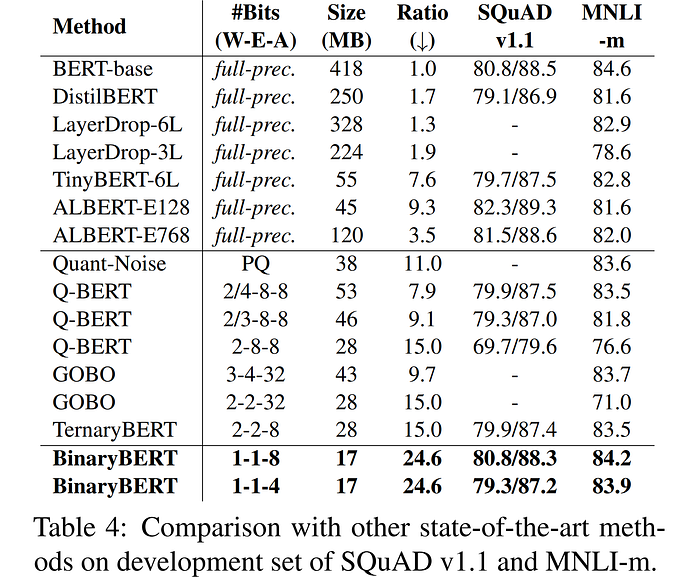
Post-Training Quantization (PTQ) of LLMs

For many reading this article, this will be the most relevant research section. Here, we review the PTQ of LLMs, which is presumably the only type of quantization that most of us can hope to use on these pretrained colossi, although we may yet be surprised. As we finally shift gears into LLM quantization, it is important to remember that because LLMs are so large, the definition of "full-precision" changes in this era to mean FP16, as this is the precision that these enormous models are typically trained in, since using FP32 would double storage requirements for minimal gains in performance. Therefore, when we discuss the compression rates of LLMs, 8-bit integer quantization only offers a 2x reduction in memory footprint compared with "full-precision" baselines. Additionally, and perhaps unsurprisingly, we'll see that networks of this scale have properties which make their quantization more difficult, namely the emergence of rare but extremely important outliers in the activations. Thus, despite the fact that LLMs are every bit as overparameterized as the more easily compressed large CNNs, their idiosyncrasies make them more difficult to quantize. Fortunately, the research community was quick to diagnose the issues and prescribe formulas which unblock the efficient and accurate PTQ of LLMs.

In mid-2022, two years after the 2020 release of the closed-source 175B GPT-3 by OpenAI, the largest open-source models were GPT-J 6B and GPT-NeoX 20B, with the 175B-scale OPT and BLOOM models yet to be released. During this period, Yao et al. from Microsoft published ZeroQuant, an early investigation into the quantization of GPT-3-style transformer models. Their method was able to achieve similar accuracy to the FP16 model with 5.2x better efficiency using INT8 quantization for both weights and activations. The authors additionally propose an efficient layer-by-layer knowledge distillation (LKD) approach to further compress the less sensitive weights to 4 bits without requiring training data, resulting in a 3x smaller memory footprint than the FP16 model. To investigate the sharp drops in performance observed when applying PTQ to large transformer models, the authors examine the highly dynamic range in the activations (tokens) which occurs between their layers, and point out that applying a uniform quantization range scaled by the min/max layer-wise activation values will lead to suboptimal representation power in the dense regions of these distributions. Similarly, the weight matrices have long-tailed ranges which will cause the fine-grain details to be lost in a small number of uniformly-spaced quantization levels. The charts below depict these layer-wise characteristics, illustrating why slicing these ranges with uniform grids would lose a lot of information.

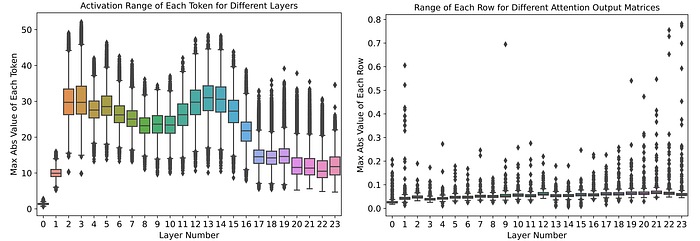
To handle the variance in these ranges, the authors propose to use group-wise quantization of the weights, and token-wise quantization of the activations. They also point out that given the large variance in activation ranges for these large transformer models, calibrating the ranges offline with a calibration dataset in a static quantization setting is likely to cause problems, and so they opt instead to calibrate token-wise min/max ranges dynamically during inference. To overcome the data movement overhead introduced by token-wise quantization, the authors build an optimized inference backend using the kernel fusion technique, which fuses each quantization operator into its previous operator (e.g. layer normalization). The authors shape their LKD approach to address three limitations of knowledge distillation of very large models, namely: the need to store both models in memory, the need to fully train the student, and the need for original training data. To circumvent these issues, the authors optimize a single layer of the quantized model at a time, and use the same set of teacher activations to feed both the quantized layer and to generate the pseudo-label through the corresponding full-precision layer. Since only these layer-wise pseudo-labels are used, there is no need for labeled data for the LKD process, and the authors show that using the original training data is unnecessary. ZeroQuant is open-sourced as part of the DeepSpeed library, which is integrated into Hugging Face's Transformers library.

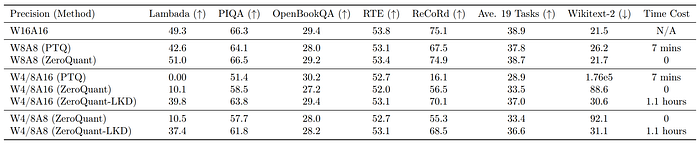
In 2022, Tim Dettmers and his colleagues introduced LLM.int8(), aka GPT3.int8(): an 8-bit integer PTQ method for ≥175B parameter scale LLMs that preserves their accuracy by using a two-part quantization procedure. First, they quantize the majority of features with vector-wise quantization granularity, using different normalization constants for each row/column inner product in the matrix multiplications. Second, the authors discover that the reason existing PTQ methods fail for transformers containing ≥6.7B parameters is the proliferation of extreme outliers in the transformer layers that occurs at these scales, which are extraordinarily sensitive to alteration and cripple model performance when removed. Thus, as the second part of their two-part procedure, the authors opt to handle these outliers separately using a mixed-precision decomposition, and demonstrate that this preserves 8-bit quantized model performance into the hundreds of billions of parameters. The code is open-sourced in the bitsandbytes library, which is also integrated into the Hugging Face ecosystem.

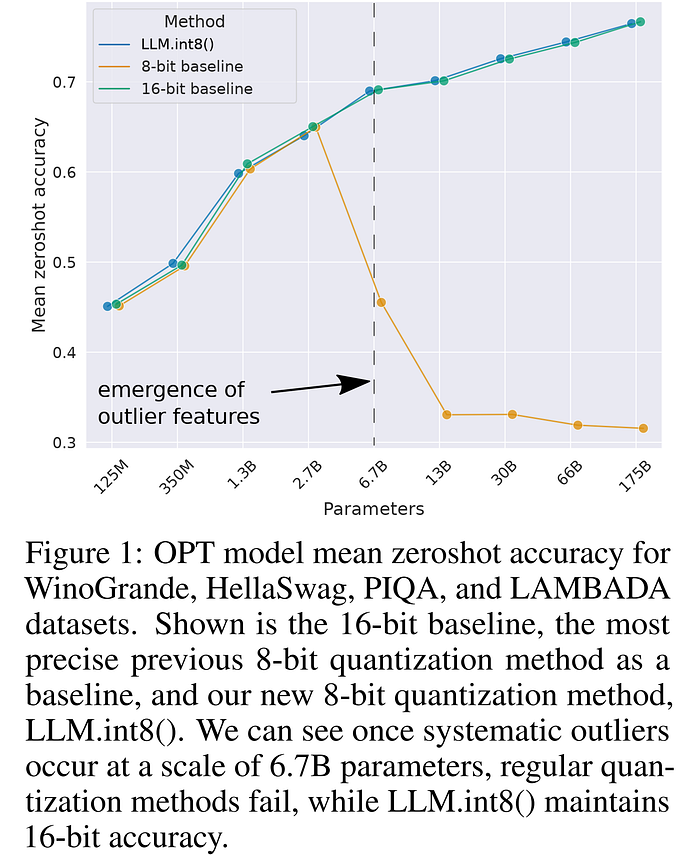
In 2022, Frantar et al. published GPTQ (also occasionally cited using the OpenReview draft title: OPTQ), a seminal work in the PTQ of LLMs, which can preserve the accuracy of pretrained models with weights quantized to 3 or 4 bit precision without requiring any retraining. The authors sought to overcome the limitations of ZeroQuant and LLM.int8() that arise from the use of "basic variants of round-to-nearest quantization," which is only effective down to 8 bits of precision. In contrast, GPTQ efficiently compresses LLMs with hundreds of billions of parameters in only a few GPU hours down to 3 or 4 bit precision with minimal loss in accuracy. To achieve this, the authors quantize weights in the network one-by-one and use approximate second-order information to adjust the remaining unquantized weights at each step, compensating for the error introduced by quantizing the current weight. This process is repeated until every weight has been quantized, with quantized weights remaining frozen as the algorithm progresses through the network.

Since GPTQ only quantizes the weights, it does not offer efficiency gains in the multiplication operations, due to the mixed-precision interactions with the non-quantized activations. However, the reduced memory footprint is essential for reducing the size of the GPU hardware required for inference, and the authors were able to run the open-source GPT-3 equivalent: OPT-175B (generously provided by Meta AI in mid-2022), for the first time on a single A100 GPU. While multiplications are not accelerated, the authors release bespoke GPU kernels which speed up inference roughly 4x on the Nvidia GPUs tested thanks to the reduced memory traffic and improved parallelism that results from moving the dequantization of weights downstream into the same GPU cores as their subsequent operations. GPTQ is open-source and has been widely adopted into several popular LLM deployment frameworks, including Hugging Face.

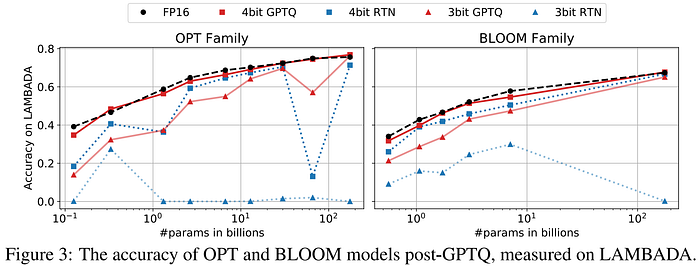
In a late-2022 collaboration between the Massachusetts Institute of Technology (MIT) and Nvidia, SmoothQuant demonstrated a method which was able to match the 8-bit PTQ performance of LLM.int8() in large models with fully quantized activations, circumventing the need for maintaining high-precision outliers by offloading their impact into the weights, which by contrast are much more uniform and easy to quantize. The diagram below provides an intuitive visual reference for this concept.

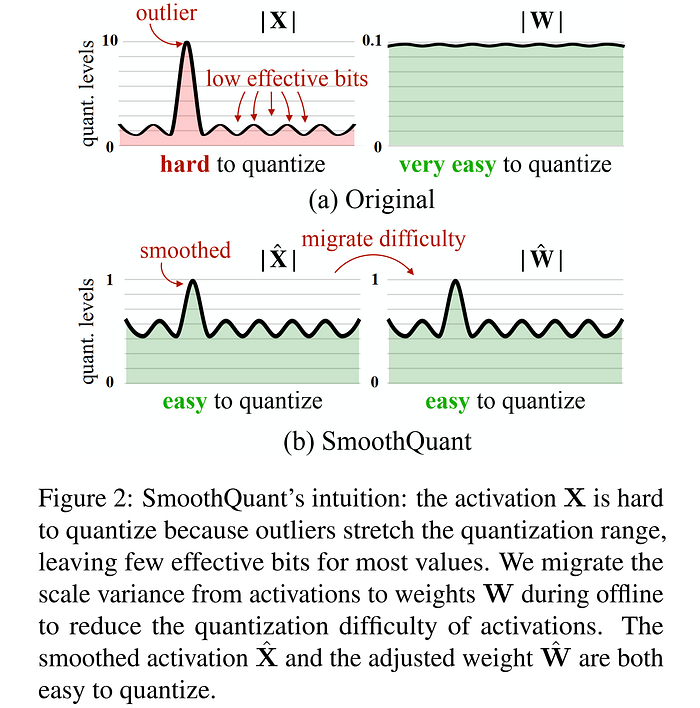
The SmoothQuant authors suggest that token-wise quantization in LLMs offers little benefit, since the additional granularity does not align with the activation outliers emerging in LMMs. They demonstrate that tokens will have high internal variance when outliers are present, since these large values will occur only in a small number of their channels; however, the channels where the outliers do occur turn out to have low variance across tokens. In other words, the outliers have channel-wise regularity, and this means that that LLM accuracy can be mostly maintained simply by using channel-wise quantization instead. However, because channel-wise quantization is incompatible with hardware accelerated INT8 general matrix multiplication (GEMM) kernels, the authors instead exploit this predictable channel-wise manifestation of outliers to adjust their corresponding weights in such a way which achieves an equivalent mathematical result while reducing the outlier values and making the activation tensors more amenable to quantization.

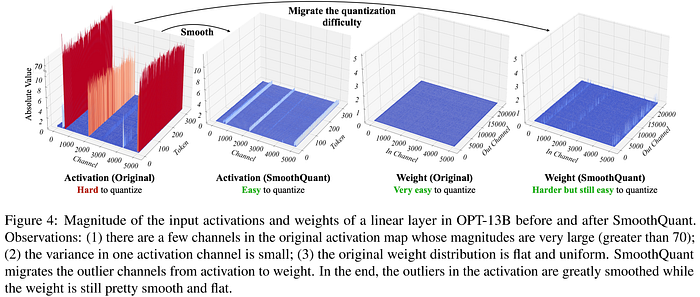
Three configurations of SmoothQuant are tested: O1-O3, which all use tensor-wise weight quantization, but differ in how they quantize the activations. O3 is the least complex, using per-tensor static quantization for the activations, where the scaling factor is calibrated offline. O2 also uses tensor-wise activation quantization, but gets a boost in performance by using dynamic quantization, which calibrates the scaling parameter online using runtime statistics. O1 explores the more complex token-wise dynamic quantization, but achieves only slightly better results than O2. Note that in the SmoothQuant method, LayerNorm and SoftMax layers are still computed in FP16, so it is not integer-only, and the approach does not work below 8-bit. Nevertheless, it marks an important stride in overcoming the particularities of LLMs which made their quantization difficult.

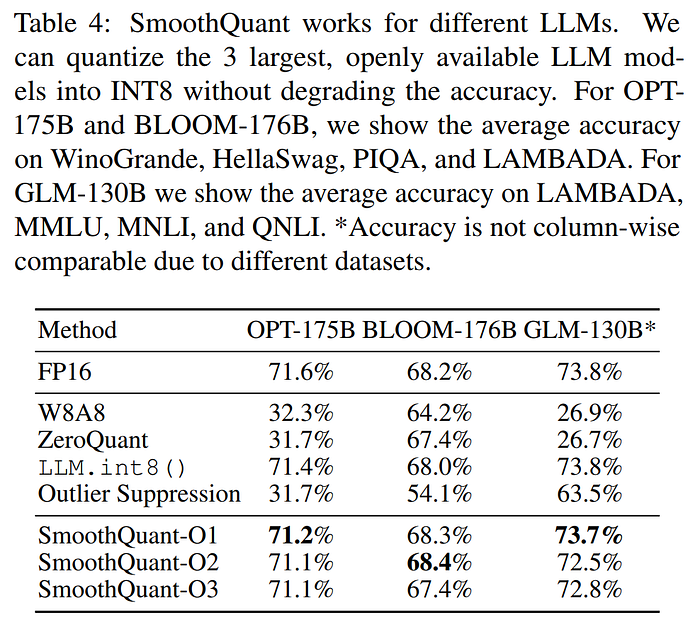
In mid-2023, the authors of ZeroQuant returned with ZeroQuant-V2, wherein they proposed to reduce quantization error by increasing granularity using a Fine-Grained Quantization (FGQ) approach they call block-k quantization, where scaling factors and/or zero points are set for each sub-vector of length k in the weight matrix rows. Additionally, the authors employ Low-Rank Compensation (LoRC) to further recover model performance using small trainable low-rank matrices to offset the layer-wise quantization error.

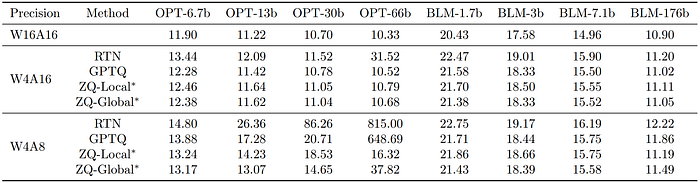
Lin et al.'s mid-2023 "Activation-aware Weight Quantization for LLM Compression and Acceleration" (AWQ) is a weight-only low-bit quantization method. The authors point out that while GPTQ is very effective, it has the potential to overfit to the calibration set, which is problematic for generalist models like LLMs. The authors point out that not all weights are equally important, and that not quantizing the 0.1–1% of highly salient network weights significantly reduces performance degradation due to quantization. To identify salient weights, the authors look at the activation signals rather than the weights themselves, and apply channel-wise scaling to minimize quantization error. The authors note that "AWQ does not rely on any backpropagation or reconstruction, so it can well preserve LLM's generalization ability on various domains and modalities without overfitting to the calibration set." The authors show that this generalization is important for maintaining performance in instruction-tuned LLMs like Vicuna and multimodal LMs (LMMs) like OpenFlamingo. Their method allows a Llama-2–70B model to fit on a 64GB Jetson Orin AGX, or 13B-scale models to run "at an interactive pace of 30 tokens per second" on the 8GB RTX-4070 GPU. The efficacy of AWQ has led to its wide adoption in popular open-source LLM serving software (more on that in upcoming the implementation guide).

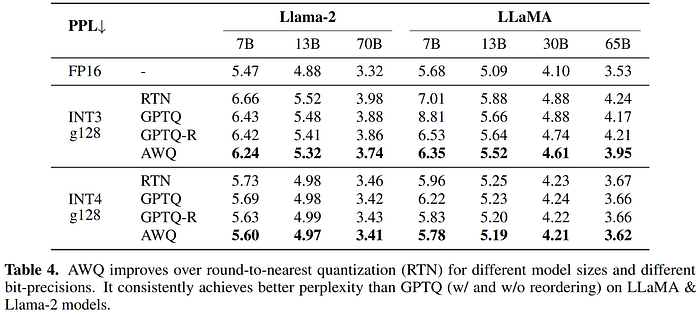
In mid-2023, SqueezeLLM exceeded the performance of GPTQ and AWQ. The authors propose a sensitivity-based non-uniform quantization, which uses second-order information to search for the optimum bit precision assignment, and a Dense-and-Sparse decomposition, which "stores outliers and sensitive weights values in an efficient sparse format." In a 3-bit setting, SqueezeLLM cuts the rise in perplexity compared with other state-of-the art PTQ methods by half. Further, the quantized models offer 2.3x faster inference than the FP16 baseline. As we've seen, most methods use uniform quantization controlled by parameters at various granularities, motivated by the simplistic application that it offers. However, as we've seen, and as the SqueezeLLM authors point out, "the weight distributions in LLMs exhibit clear non-uniform patterns," signaling that non-uniform quantization will naturally provide better representations. Moreover, the authors argue that since most works only quantize weights and perform arithmetic in FP16, the advantage of uniform quantization is not fully realized anyhow, and that non-uniform quantization is preferable for its lower impact on outliers, which preserves representation power at lower precision. Further, the authors decompose and isolate the weight outliers in efficient sparse representations, thereby making the distributions more amenable to quantization. Code for SqueezeLLM is available on GitHub.

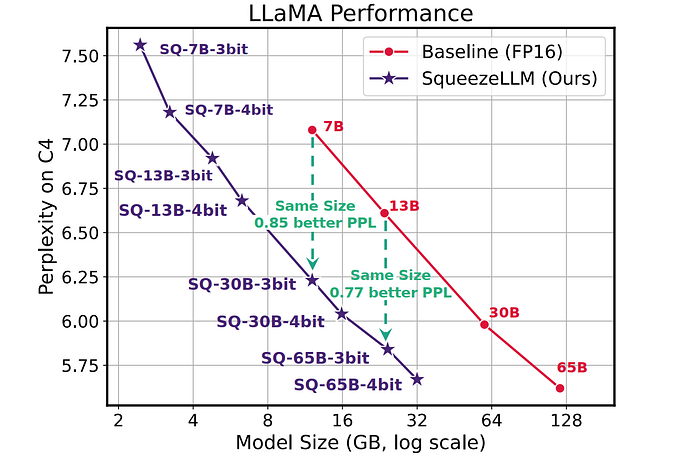
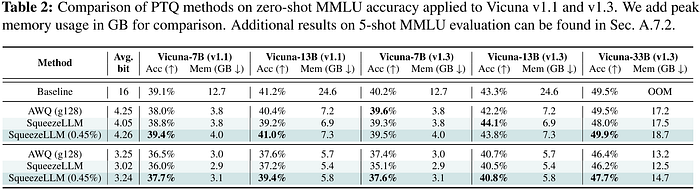
In late 2023, Mobius Labs GmbH open-sourced an extraordinarily efficient and accurate zero-shot PTQ approach which works well down to very low precision, called Half-Quadratic Quantization (HQQ). This method is able to quantize the large LLaMA-2–70B model 50x faster than GPTQ, taking only 5 minutes on the GPU tested. The authors point out that the limitation of GPTQ and AWQ is the need for calibration data for minimizing error between the layer outputs, which risks overfitting to the calibration set and requires compute time and resources. To sidestep this, HQQ minimizes quantization error in the weights rather than activations, but does so in a way which more accurately captures the impact of the outliers by using a sparsity-encouraging loss function which they decompose into two solvable sub-problems using a Half-Quadratic solver, iteratively reaching an optimal solution for the group-k quantization parameters in closed-form, without the need for data, by performing alternative optimization of the two sub-problems. Compared with the popular data-free LLM.int8() method from bitsandbytes, HQQ consistently produces models with lower perplexity. Further, while HQQ is 50x faster to perform than GPTQ and around 25x faster than AWQ, the results are better than or equivalent to these data-dependent methods, particularly when using less than 4 bits of precision. The HQQ code is open-sourced, and some pre-quantized models are available on the Hugging Face hub. While using HQQ models within the Hugging Face ecosystem is straightforward, the HQQ integration in the optimized vLLM inference engine is still "experimental" at the time of this writing.

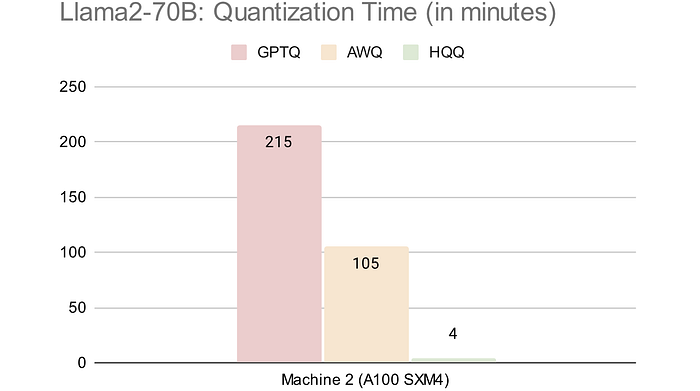
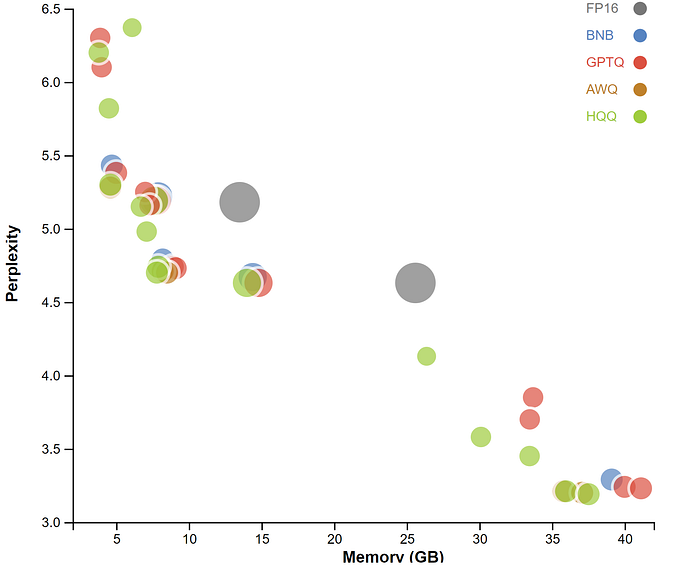
In December of 2023, SmoothQuant+ set a new state-of-the-art in 4-bit uniform PTQ. The authors address the limitations of AWQ, which has a search space that scales with the number of layers, and does not take the problem of error accumulation "into account during the searching process, which makes the search speed slow and the model accuracy degraded." Further, they assert that the weight quantization loss is amplified by the activation outliers, and smoothing their values with weight adjustments can therefore greatly reduce overall quantization error. The authors provide custom W4A16 kernels for the popular vLLM inference engine, and design the SmoothQuant+ implementation to work without requiring a preprocessing step from the user, allowing them to load FP16 models directly from the Hugging Face hub, with the quantization process applied automatically as the model is moved onto the GPU. Unfortunately, as of the time of this writing, the SmoothQuant+ algorithm code has yet to land on the public GitHub page, and the integration into vLLM is not yet online.

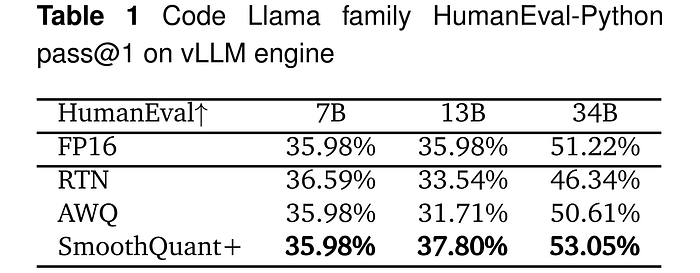
In April 2024, Park et al. published the latest version of their LUT-GEMM paper. In this work, the authors point out that weight-only quantization typically enables higher compression rates at a given level of accuracy compared with quantizing both weights and activations, since memory traffic is highly dominated by the weights, and the activations are much more sensitive to quantization. However, as we've discussed, this comes at the cost of losing integer-only benefits and requires dequantizing the weights before multiplication. To address this, LUT-GEMM is a kernel designed to enable the matrix multiplication directly between quantized weights and unquantized FP16 activations without requiring a dequantization step.

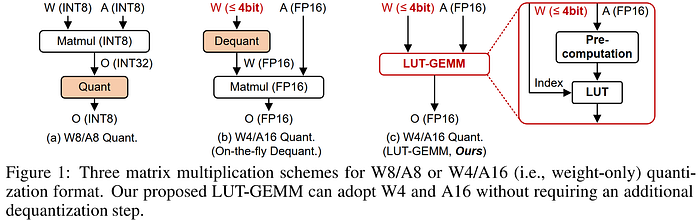
LUT-GEMM expands on the binary-coding quantization (BCQ) format used in XNOR-Net, which enables the use of simple arithmetic operations. While BCQ was originally designed for non-uniform quantization, the authors demonstrate that it generalizes to uniform quantization as well through the addition of a bias term, which greatly increases representational capacity. The authors construct a LUT of potential sub-vector products, as there are a limited number of possibilities, and then index them using the sub-vectors encountered during run-time rather than carrying out the operations that generate them, greatly improving efficiency. Using their quantization scheme, they demonstrate a 2.1x inference speedup over GPTQ on a single GPU. LUT-GEMM is the default quantization scheme used by the powerful MLC-LLM inference engine, which we will learn more about later.

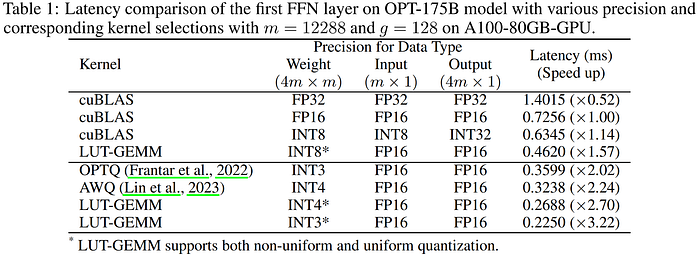
In this section, we have seen the legacy of PTQ come to fruition in the era of LLMs. These gargantuan models are extremely cost prohibitive to train, and thus necessitate the innovation of efficient one-shot or zero-shot quantization approaches like never before. Accordingly, researchers have provided extremely effective approaches to the open-source community, with bitsandbytes (LLM.int8), GPTQ, and AWQ becoming particularly popular, and the recently released HQQ offering a powerful new data-free alternative. In the implementation guide, we will weigh the comparative pros and cons for choosing between these quantization algorithms. But first, let's complete our research journey by daring to explore the QAT of LLMs, since we know that QAT achieves superior quantization outcomes by its very nature, and perhaps we'll be pleasantly surprised at how accessible some of these methods actually are.

Quantization-Aware Training (QAT) of LLMs

In our final research section, we review the intimidating domain of QAT methods for LLMs. LLaMA-2 is said to have cost north of $20 million to train, so should we even involve ourselves here? While some of the approaches here may not be accessible to us as individuals, they are important to understand for a broader understanding of what is possible. One question that arises is, if QAT is the most effective way of generating efficient, low-bit models without affecting their performance by incorporating quantization into the training process, then why shouldn't the companies spending tens of millions of dollars to train open-source foundation models use these techniques as a component in their release strategy? What proportion of LLaMA-2 users are ever using full-precision weights, and wouldn't it be better to make large models more amenable for quantization, since we know that the vast majority of deployments will be using it? This section may help us develop a more educated opinion on these matters.

Liu et al.'s mid-2023 "LLM-QAT" was the first exploration of QAT in LLMs. The authors pointed out that the current state-of-the-art PTQ approaches did not protect accuracy below 8 bits of precision, and that while QAT is probably necessary to preserve performance at lower precisions, no previous work had sought to investigate QAT of LLMs for the reasons we already know: the implied necessity of huge amounts of data and compute, as well as some more nuanced reasons, such as the difficulty of replicating the training processes of instruction-tuned LLMs. To circumvent these challenges, the authors introduce a data-free knowledge distillation method that uses generations from the pretrained model to serve as the training data, which provides better preservation of the output distribution, even when compared to training with large subsets of the original training data.

The LLM-QAT authors find that even a relatively small set of 100k synthetic samples is sufficient to distill quantized models, which can be done with reasonable amounts of compute. They find that stochastic sampling the most probable tokens at each generation step is essential to add noise into the data. Unlike most previous works in transformer quantization, LLM-QAT investigates quantization of the intermediary activation vectors stored in the KV cache, which is particularly beneficial with long sequences. The fact that the authors limit their investigation to LLaMA models ≤30B parameters echoes the underlying expense of QAT; that being said, the authors benchmark a plethora of mixed-precision configurations in their study, showing that their method is able to preserve LLM performance significantly better than GPTQ and SmoothQuant in low-bit settings. However, at higher precisions, the results are mostly equivalent, which indicates that the PTQ approaches are more favorable when higher precision is tolerable, due to their simplicity. Nevertheless, the ability of LLM-QAT to efficiently retrain LLMs to low-bit settings without training data and preserving performance is very exciting, particularly as LLMs become more parameter efficient. The code is available on GitHub.

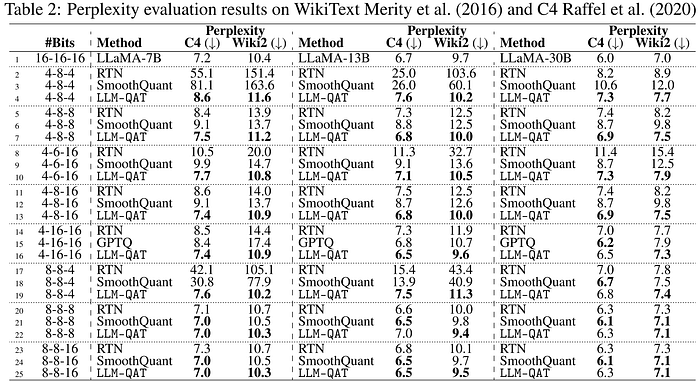
In 2023, Xi et al.'s concisely titled "Training transformers with 4-bit integers" introduced a method to train transformer models with all multiplications carried out in 4-bit integer arithmetic. To do this, the authors handle the important outliers in the activations during the forward pass using their proposed Hadamard quantizer, which quantizes a block diagonal Hadamard matrix transformation of each activation matrix. This transformation is beneficial because it spreads the outlier information into nearby matrix entries, reducing the their numerical range, and making the matrix amenable to quantization. During backpropagation, the authors propose to save the calculations by not computing small gradient rows in the activations, and use the saved computation to split the most informative gradients into a lower 4 bits and higher 4 bits, preserving their detail using two rows which together create an 8-bit representation. Using this approach, the authors achieve accurate training of transformers using all-4-bit arithmetic without requiring custom numerical formats like FP4, meaning that the gains can be realized on contemporary hardware. The authors demonstrate their INT4 matrix multiplication operator is 2.2x faster than FP16 training, and reduces total training time by 35.1%, while coming close to matching baseline performance across a variety of tasks and transformer models. While this study is focused on BERT and Vision Transformer (ViT) rather than LLMs, it's appropriate to cite in this section, as it marks a major landmark in low-precision training of large transformer models, showing us what is possible. Further, it is surely only a matter of time before this type of technique it is applied to LLMs. The authors have released their code on GitHub.

Famously in 2023, Tim Dettmers and his colleagues at University of Washington broke new ground with QLoRA, which uses the efficient Low-Rank Adaptation fine-tuning technique to backpropagate gradients from a frozen, quantized 4-bit LLM through the trainable low-rank matrices to fine-tune a 65B model with only 24 hours of training a single 48GB GPU, while maintaining baseline FP16 performance. QLoRA substantially reduces the amount of hardware needed to fine-tune LLMs, marking a substantial landmark in the democratization of this technology. To achieve this, the authors find that using a novel 4-bit NormalFloat (NF4) data type, which is theoretically optimal for quantizing normal distributions, yields better empirical results than either INT4 or FP4 types. The authors also investigate the use of double quantization, in which the quantization parameters are also quantized, saving an average of 0.37 bits per parameter (3GB in a 65B model). Highlighting the efficiency of their approach, the authors exhaustively test QLoRA on over 1000 models using several instruction tuning datasets. The authors use their QLoRA method to train a family of Guanaco models. A notable advantage of using any variant of LoRA is that the pretrained model remains unchanged, with the fine-tuning fully captured in the low-rank adapter matrices. This means several sets of these adaptors can be trained for multiple use-cases without full model retraining. Fine-tuning with QLoRA is possible through Hugging Face Transformers via the bitsandbytes library, and the original QLoRA repo is available on GitHub.

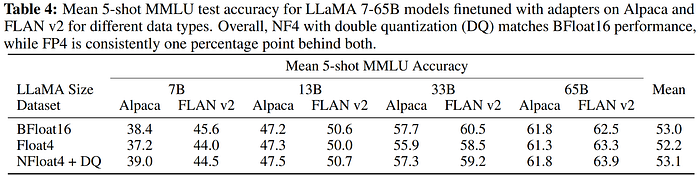
Extreme Quantization of LLMs

Recently, the allure of extreme quantization has made its way into LLM research. As we saw earlier in the section on CNN quantization, neural networks can perform surprisingly well with binary or ternary weights with dramatically reduced memory traffic and computational complexity, as the weights occupy far fewer bits and the multiplication operations can be replaced with additions and subtractions. While extreme quantization of LLMs is a still a nascent field, recent work has demonstrated compelling results which will surely inspire the research community to develop this methodology into maturity. In this section, we will see the sparks of a dawning era of low-bit LLM training.

In 2023, the authors of BitNet introduced a 1-bit transformer architecture that was suitable for use in LLMs. They introduce a BitLinear layer which can be swapped in for the nn.Linear layers, and train binary weights from scratch to achieve competitive performance with full-precision baselines, finding that the resulting transformers also exhibit a similar scaling law to their full-precision counterparts, while using operations that require far less power. Activations are quantized to 8 bits, and the optimizer states and gradients are still carried out in full-precision. The authors admit that since their implementation performs operations in FP16/BF16, there is no actual training acceleration, but they propose that low-precision FP8 GEMM CUDA kernels could be used to accelerate the forward and backwards passes, although they leave this for future work.

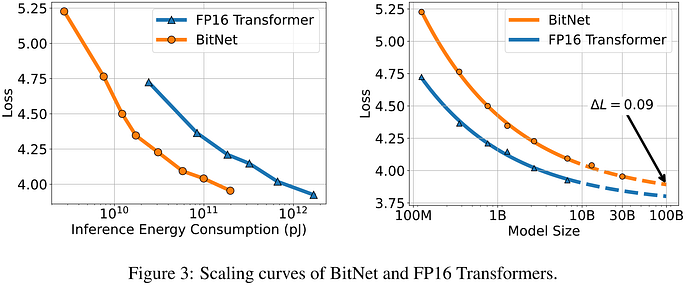
Following up in 2024, the BitNet authors published BitNet b1.58 which expanded their work into the use of ternary {-1, 0, 1} weights, adding the zero value into the previous 1-bit BitNet system by tuning a γ threshold parameter that clamps small values to zero. As we learned with ternary CNNs, adding in the zero value in the weights causes no increase in operational complexity, since multiplications can still be replaced by addition/subtraction, but it markedly improves performance by enabling the weights to perform "feature filtering," at the expense of doubling the number of bits per weight from 1 to 2. In either case, since the weights are smaller, the transfer from DRAM to SRAM is easier, and memory traffic is reduced. The authors use symmetrical quantization for easier kernel optimization, quantize activations to 8-bit, and quantize the KV cache to 4-bit. Using this approach, the authors train ternary networks from scratch which match baseline FP16 performance in both perplexity and task performance.

For detail on the code and implementation of BitNet b1 (binary) and b1.58 (ternary) approaches, the reader should see the Training Tips, Code, and FAQ PDF file. However, the code offered there does not detail the low-bit kernel to use for inference. Fortunately, the open-source community has developed this GitHub repo with a full implementation, complete with custom kernels and pip install. It's important to note that while BitNet is a powerful step into extreme quantization of LLMs, the binarization and ternarization is not being fully exploited in these implementations, as multiplications are still in half-precision during training, and the custom kernels being used to accelerate inference are FP8. However, we learned earlier that the most pronounced benefit of using binary/ternary weights was that matrix multiplications could be replaced with far more energy-efficient integer addition/subtraction operations, which translates directly to faster computation, but that has not been explored here for either training or inference, leaving an open lane for future work.

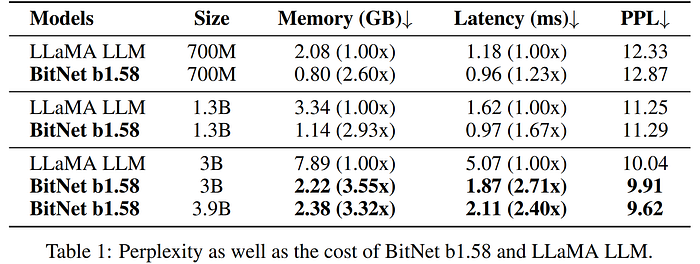
Practitioner's LLM Quantization Guide

In this section, we will discuss practical implementation of quantization to optimize our workflows. As we've seen, quantization can be applied during training or as a post-processing step in model development, and the choice between these will depend on the model and use case. To become educated practitioners in quantized workflows, we will first review the current tool sets available to us, along with their strengths and weaknesses. Then, we will use what we've learned to develop a decision tree that will help us to align our goals with the methods available.

A popular and easy way to experiment with transformer development and inference is using the Hugging Face Transformers library (along with their model hub, which operates like a GitHub repo for deep learning models, allowing you to easily push your model checkpoints and pull them for use on other machines with just a few lines of code. While this is an amazing interface for people who can operate Python code, it does not provide a non-code user interface (UI) for using the models, and while this library can be used as a capable backend for inference, it generally serves better as a development ecosystem, since more optimized libraries provide faster backend serving, as we will see. However, on the training side, the integration of the bitsandbytes library for enabling efficient quantized training with QLoRA through the intuitive interface of Hugging Face's Transformers library makes it a very powerful tool for model development.

Starting in July 2019, Nvidia offered the FasterTransformer library to optimize inference throughput of transformer models (originally focused on BERT), and used this to back the TensorRT SDK for their devices. Subsequently, this project has evolved into TensorRT-LLM (aka TRT-LLM), which is a Python API built to look similar to PyTorch, and includes support for GPTQ, AWQ, and an implementation of the SmoothQuant technique. These libraries are specifically engineered to optimize inference on Nvidia hardware or their Triton inference server, so while it is very effective for those using these, it is not a general-purpose quantization library. That being said, for those seeking to use multi-GPU settings with Nvidia hardware, it may be the right choice. The library includes pre-built versions of many popular open-source models, but users can also quantize custom models using the API.

Meanwhile, Georgi Gerganov's Machine Learning library (GGML), a pure C library designed to accelerate LLM inference on Apple devices, was created in September of 2022, and has been steadily developing since. GGML uses quantization to create structured binary model files that can be used to perform optimized tensor calculations on various hardware. While the library is specifically tailored for Apple silicon, it now provides support for accelerating inference on x86 architectures and GPUs as well. The GGML library provides the backend for the highly popular llama.cpp inference library, which then in turn provides backend support for frontend libraries like Ollama and LM Studio. GGUF is the new and improved file format offered by the GGML library. The drawback to using these compression formats is that they mandate the use of llama.cpp for inference, which is not optimal for many hardware architectures, particularly non-Apple devices. However, llama.cpp has added support multi-GPU/CUDA hardware setups, so user-friendly tools like Ollama are quite effective, even if not the fastest.

vLLM is a powerful inference engine that was introduced in Kwon et al. 2023, which uses optimized CUDA kernels to accelerate performance on Nvidia and AMD GPUs. The authors point out the fact that the one-by-one sequential token generation process of LLMs is memory-bound, and thus underutilizes the computation power of GPUs. To address this, they build the vLLM serving engine on top of their proposed PagedAttention algorithm, which improves memory efficiency of the KV cache to avoid wasted space, crucial for increasing the maximum batch size on a given piece of hardware. Shows 2–4x better throughput than FasterTransformer, with the advantage more pronounced with larger and more complex models and larger sequences. vLLM has seamless integration with Hugging Face models, and supports multi-GPU workflows. The engine works well with GPTQ, AWQ, SqueezeLLM, and FP8 KV cache quantization, allowing models quantized through any of these methods to benefit from the speed benefits of PagedAttention. SmoothQuant+ integration is coming soon.

MLC-LLM is a powerful, universal deployment solution for optimized native deployment of quantized models on multiple types of hardware, including Apple, Nvidia, AMD, Intel, and mobile devices. At the time of this writing, it appears to be the fastest and most general serving engine available, and is preferred by the Jetson AI Lab for its superior throughput. The MLC-LLM library offers a set of prebuilt models, as well as the option to compile new models for use with the library.

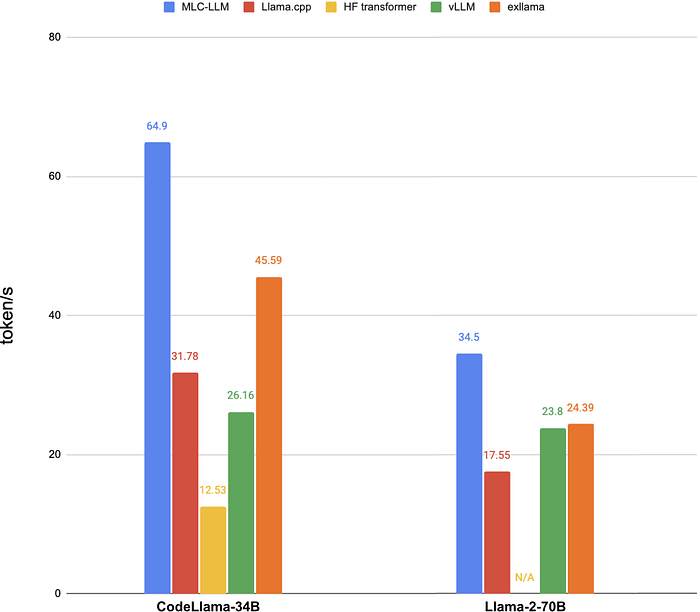
LLM Quantization Decision Tree

In this article, we have covered a lot of methodology which creates a dizzying list of design options for quantization. Fortunately, a handful of open-source inference engines have put the most useful of these tools at our fingertips in some intuitive form factors. This decision tree can be used as a very basic rule-of-thumb based on the intended use case and deployment environment, but is not an exhaustive list of considerations. It is intended to give practitioners a launching point for implementing quantization in their workflows.

• Q: Are you deploying a pretrained model on CPU or at the edge? A: Yes — For Apple users, go with GGML-based inference (llama.cpp, Ollama, LM Studio). For Android and x86 hardware, use MLC-LLM. No — Go to next question.
• Q: Will you be serving simultaneous batched requests? A: Yes — Use vLLM, it is specifically optimized for this. No — Go to next question.
• Q: Are you deploying a pretrained model on a GPU? A: Yes — MLC-LLM appears to provide state-of-the-art throughput on Nvidia and AMD GPUs, and while it also supports Apple GPUs, llama.cpp has the pedigree for being optimized for Apple hardware, so a comparison is warranted. For Nvidia and AMD GPUs, the forthcoming integration of SmoothQuant+ in the vLLM library will be worth a test when available. No — Go to next question.
• Q: Are you fine-tuning a quantized LLM? A: Yes — Use QLoRA. This is the most efficient way to enable a quantized LLM to perform new tasks or recover lost performance due to quantization. It is used easily in Hugging Face Transformers. No — Go to next question.
• Q: Are you training a foundation model? A: Yes — Try using BitNet to prototype or develop foundation models, as it is far cheaper to train and provides competitive performance to full-precision baselines. Even better, try ensembling these low-bit models.

This checklist should provide the average user with a solid guide on where to look given their circumstance. For a more comprehensive guide into LLM inference frameworks, check out this post from Sergei Savvov.

Conclusion

In this article, we've seen some incredible feats in quantization research. We've seen lossless 8-bit quantization grow into a boring baseline, binary CNNs nearly match their full-precision counterparts, large transformer models trained in 4-bits of precision, and the rise of extreme quantization in LLMs. We've seen that INT8 PTQ is fully mature, easily matching full-precision baselines, with wide integration into most open-source libraries, so it is arguable that no one should be serving models using floating point data types >8bit. In the case of LLMs, which are often released in FP16, this lossless INT8 quantization halves memory footprints and provides "free lunch" compression. Further, quantizing at lower precision has been achieved with minimal performance loss, and for many practical use cases, an accelerated and seamless user-experience will be a welcome trade-off for a slight drop in accuracy. The idea of ensembling extremely low-bit networks like we saw in the BENN paper is very compelling, especially as we now see the rise of extreme quantization in LLMs, which may soon benefit from this methodology.

We've seen a variety of quantization approaches, catering to different use cases with a range of complexities, and watched their growth through time, revealing which approaches have caught on and become popularized in the open-source community. While PTQ and ZSQ have become very effective, QAT is still fundamentally the most performant approach because it incorporates quantization into the network training process. While this is much more resource intensive, and seems to preclude its use on LLMs by the average practitioner, the ingenuity of QLoRA allows us to blur the line between PTQ and QAT by training only a small number of parameters in low-rank matrices to recover loss due to quantization. We've seen PTQ recently become effective down to 2-bits of precision with the HQQ method, and we've seen that binary and ternary LLMs can be trained from scratch to nearly match the performance of their full-precision counterparts.

Congratulations on making it to this point. Familiarized with the works reviewed in this article, you now have an expert knowledge on neural network quantization. This survey was not for the faint of heart, but there was no need for a superficial summary of quantization methods in 2024. For proper ML practice, we require a comprehensive foundation of knowledge to make educated decisions that weigh all potential options, as well as the pros and cons of our chosen methodology. Quantization of neural networks is an extremely prolific field of research build on a rich legacy, which poses a daunting research challenge for those wanting to achieve a wholistic understanding. Hopefully, this article provides an accessible, self-contained, and comprehensive resource to practitioners in the field, as well as some effective suggestions for which tools are the best for their common use cases.

Future Work

BitNet does not use low-precision computation during training, and also does not fully capitalize on the binarization or ternarization of its weights, since it does not replace multiplications with addition/subtraction operations. These factors are crippling its ability to realize its true value. The legacy of work in the extreme quantization of CNNs should be applied to binarize the actual mathematics and make the operations used by BitNet more efficient. Further, once optimized kernels are established for BitNet, we should start investigating the ensembling of these low-bit LLMs, as we saw that this was highly effective with CNNs in the BENN paper.

HQQ is a very efficient algorithm for accurate data-free (zero-shot) PTQ, but so far only one optimized inference engine (vLLM) has started adding experimental support for running these models. Further, there are currently no benchmarks on the inference throughput of models quantized using HQQ compared to other methods. Both of these items are open areas for future work.