RNNs stand out from other types of neural networks because they handle sequences of inputs. This capability allows them to take on tasks that depend on the order of the data, such as forecasting stock market trends, monitoring patient health over time, or predicting the next word in a sentence. This makes them extremely valuable for many cutting-edge AI applications. In this article, we will dive into their architecture and math and create them from scratch in Python.

Index

1: Introduction

2: RNN's Architecture ∘ 2.1: The Structure of RNNs ∘ 2.2: Key Operations in RNNs

3: Challenges in Training RNNs ∘ 3.1: Vanishing Gradients ∘ 3.2: Exploding Gradients ∘ 3.3: Gradient Clipping ∘ 3.4: Adjusted Initialization Strategies

4: Building RNN from Scratch ∘ 4.1: Defining the RNN Class ∘ 4.2: Early Stopping Mechanism ∘ 4.3: RNN Trainer Class: ∘ 4.4: Data Loading and Preprocessing ∘ 4.5: Training the RNN

5: Advanced RNN Architectures ∘ 5.1: Long Short-Term Memory Networks (LSTMs) ∘ 5.2: Gated Recurrent Units (GRUs) ∘ 5.3: Bidirectional RNNs

6: Conclusion · References

1.1: Introduction

Recurrent Neural Networks (RNNs) are a type of neural network tailored for sequential data. Unlike traditional feedforward neural networks that process each input independently, RNNs can remember previous inputs. They achieve this by feeding the output from one step back into the network in the next step. This makes this architecture ideal for tasks where the sequence or context of the data is crucial, such as predicting time-series data, processing natural language, and more.

In our previous article, "The Math Behind Fine-Tuning Deep Neural Networks", we explored the details of neural networks, focusing on how they are mathematically structured and practically applied. We looked at various ways to optimize them, the complexity of their layers, and how to implement them using Python in Jupyter Notebooks. If you're new to this topic or need a quick refresh, revisiting that content will help you better understand the more advanced concepts we will discuss about RNNs.

2: RNN's Architecture

2.1: The Structure of RNNs

Recurrent Neural Networks differ from other neural networks mainly because they have an internal state or memory that keeps track of the data they have processed. Basically, an RNN is made up of three key components: the input layer, one or more hidden layers, and the output layer.

Input Layer This layer takes in sequences of inputs over time. Unlike feedforward networks that process all inputs at once, RNNs handle one input at a time for each time step. This sequential processing allows the network to maintain a dynamic that changes over time.

Let's denote X_t​ as the input at time step t. This input is fed into the RNN one step at a time.

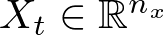
where n_x​ is the number of units (neurons) in the input layer.

For example, this is how we would initialize the input layer in Python:

self.weights_ih = np.random.randn(input_size, hidden_size) * 0.01

Here input_size is the size (number of neurons) of the input layer. hidden_size is the size of the hidden layer. self.weights_ih is the weight matrix connecting the input layer to the hidden layer, initialized with normally distributed random values, scaled by 0.01 to keep them small.

Hidden States Hidden layers are crucial in an RNN because they process not only the current input but also retain information from previous inputs. This information is stored in what we call the hidden state and is carried forward to influence future processing. This ability to carry forward information is what gives RNNs their memory capabilities.

The hidden state h_t​ at time step t is computed based on the current input Xt​ and the previous hidden state h_(t−1)​. This is expressed as:

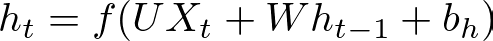
where:

• h_t ​​ is the hidden state at time step t,
• W is the weight matrix for the hidden layer,
• b_h​ is the bias vector for the hidden layer,
• f is a nonlinear activation function, often tanh⁡tanh or ReLU.

Let's set the hidden states initially to zero: h = np.zeros((1, self.hidden_size)). This initializes the first hidden state h with zeros, preparing it for the first input in the sequence.

As the RNN processes each input in the sequence, the new hidden state is computed using both the current input x and the previous hidden state h. This happens in the loop inside the forward method, which we will build later:

for i, x in enumerate(inputs):
    x = x.reshape(1, -1)  # Ensure x is a row vector
    h = np.tanh(np.dot(x, self.weights_ih) + np.dot(h, self.weights_hh) + self.bias_h)
    self.last_hs[i + 1] = h

In each iteration of the loop, the current input x is transformed into a row vector and then multiplied by the input-to-hidden weight matrix self.weights_ih.

Simultaneously, the previous hidden state h is multiplied by the hidden-to-hidden weight matrix self.weights_hh. The results of these two operations are summed with the hidden bias self.bias_h.

The sum is then passed through the np.tanh function, which applies a nonlinear transformation and yields the new hidden state h for the current timestep.

This new hidden state h is stored in a dictionary self.last_hs with the current timestep as the key. This allows the network to "remember" the hidden states at each step, which is essential for the backpropagation through time (BPTT) during training.

Output Sequences RNNs are flexible in how they output results. They can output at each timestep (many-to-many), produce a single output at the end of a sequence (many-to-one), or even generate a sequence from a single input (one-to-many). This flexibility makes RNNs useful for a range of tasks like language modeling and time-series analysis.

The output at each time step O_t​ can be calculated from the hidden state. For a many-to-many RNN:

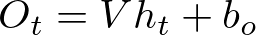
​where:

• O_t​​ is the output at time step t,
• V is the weight matrix for the output layer,
• b_o is the bias vector for the output layer.

For a many-to-one RNN, you would only compute the output at the final time step, while for a one-to-many RNN, you would start with a single input to generate a sequence of outputs.

The computed output Ot​ is often passed through a softmax function if the RNN is used for classification tasks to obtain probabilities of different classes.

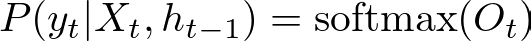
where P(y_t​ ∣ X_t​, h_(t−1​)) is the probability of the output yt​ given the input Xt​ and the previously hidden state h_(t−1​).

The sequence of operations from input to hidden state to output captures the essence of RNNs' ability to maintain and utilize temporal information, allowing them to perform complex tasks that involve sequences and time.

RNNs have a loop within them that allows information to flow from a later stage of the model back to an earlier stage. This looping mechanism is what enables them to process sequences of data: it allows outputs from the network to influence subsequent inputs processed by the same network. This fundamental difference is what enables RNNs to perform tasks that involve sequences and time-series data effectively.

2.2: Key Operations in RNNs

Understanding how Recurrent Neural Networks (RNNs) operate is essential for using them effectively and improving their performance. Let's break down the main operations within an RNN:

2.2.1: Forward Pass In the forward pass, an RNN processes data one step at a time. For each timestep, it combines the current input with the previous hidden state to compute the new hidden state and the output. The model use specific functions that are inherently recurrent, meaning each output depends on the preceding computations. Functions like the sigmoid or tanh are commonly used to introduce non-linearity, helping to manage how information is transformed within the hidden layers.

Here's how the math plays out:

Initially, we set the hidden state h to a vector of zeros. This is represented mathematically as:

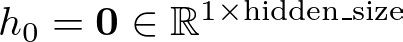
Or in Python terms:

h = np.zeros((1, self.hidden_size))

As we move through each input in the sequence, we compute the new hidden state at time step t, denoted h_t​, based on the previous hidden state h_(t−1)​, the current input x_t​, and the associated weights and biases:

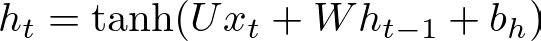
where we can define U, W, and b_h as:

self.weights_ih = np.random.randn(input_size, hidden_size) * 0.01
self.weights_hh = np.random.randn(hidden_size, hidden_size) * 0.01
self.weights_ho = np.random.randn(hidden_size, output_size) * 0.01

Here:

• U is self.weights_ih, the weight matrix connecting inputs to the hidden layer.
• W is self.weights_hh, the weight matrix connecting the hidden layer at one timestep to the next.
• b_h​ is self.bias_h, the bias term for the hidden layer.
• tanh represents the hyperbolic tangent function, introducing non-linearity into the equation.

This mirrors the loop in the forward method that iterates over each input.

The output at time step t, which we call y_t​, is then calculated from the hidden state using another set of weights and biases:

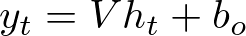
​In this case:

• V is self.weights_ho, the weight matrix from the hidden layer to the output layer.
• b_o​ is self.bias_o, the output layer bias.

The code y = np.dot(h, self.weights_ho) + self.bias_o corresponds to this equation, which generates the output based on the hidden state at the final timestep.

Backpropagation Through Time (BPTT) Training RNNs involves a special kind of backpropagation called BPTT. Unlike traditional backpropagation, BPTT extends across time — it unfolds the entire sequence of data, applying backpropagation at each timestep. This method calculates gradients for each output, which are then used to adjust the weights and reduce the overall loss. However, BPTT can be complex and resource-intensive, and it's prone to issues such as vanishing and exploding gradients, which can interfere with the network's ability to learn from data over longer sequences.

Given a sequence of T timesteps and assuming a simple loss function L at each timestep t, such as mean squared error for regression tasks or categorical cross-entropy for classification tasks, the total loss L_total​ is the sum of the losses at each timestep:

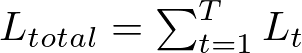
​To update the weights, we need to calculate the gradient of L_total​ with respect to the weights. For the weight matrices U (input to hidden), W (hidden to hidden), and V (hidden to output), we have:

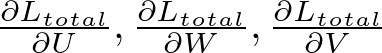
​​These gradients are computed using the chain rule. Starting from the final timestep and moving backwards:

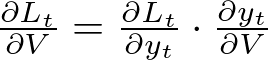
Where:

• ​∂L_t/∂y_t​​ is the derivative of the loss function at timestep t with respect to the output y_t​.
• ∂y_t/∂V​​ can be directly calculated as the hidden state h_t​ because y_t​ = V_h_t​ + b_o​.

For W and U, the calculation involves the recurrent nature of the network:

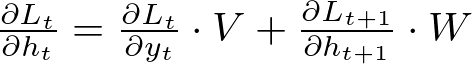
Here, ​∂Lt+1​ / ∂ht+1​ refers to the gradient of the loss at timestep t+1 with respect to the hidden state at t+1, which in turn depends on the hidden state at t. This recurrence relation forms the crux of BPTT.

Weight Updates With the gradients calculated, the weights are updated using an optimization algorithm such as stochastic gradient descent (SGD):

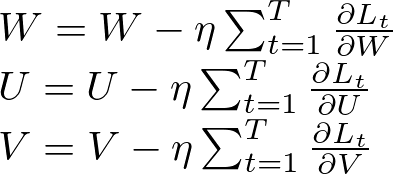
​​Where η is the learning rate.

Loss Functions Specific to Sequential Data The type of loss function used can greatly influence how an RNN learns. For regression tasks, such as predicting future values in a time series, mean squared error (MSE) is typically used. For classification tasks, like predicting the next word in a text, categorical cross-entropy is more common. These loss functions are calculated at each timestep, and the total loss for a sequence is the sum of these individual losses, giving a clear picture of the RNN's performance across the entire sequence.

3: Challenges in Training RNNs

Training RNNs presents unique challenges, particularly the vanishing and exploding gradient issues. Understanding these problems is critical to optimizing RNNs effectively:

3.1: Vanishing Gradients

When training RNNs using backpropagation, the gradients of the loss function are passed backward through the network to update the weights. In deeper network layers, these gradients can decrease exponentially as they propagate back through each layer, due to their multiplication by small numbers (less than one). This reduction can cause gradients to approach zero, making it difficult for the network to learn and update its weights effectively, especially when learning dependencies over long sequences.

The issue of vanishing gradients is represented mathematically by the successive multiplication of gradients that are less than one in magnitude during backpropagation. In a simple RNN, this can be expressed as:

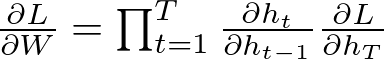
​where:

• L is the loss function,
• W is the weight matrix of the RNN,
• h_t​ is the hidden state at time step t,
• T is the total number of timesteps,
• ∂h_t/​∂h_(t-1)​​ represents the gradient of the current hidden state with respect to the previous hidden state,
• ​∂L/∂h_T is the gradient of the loss with respect to the final hidden state.

If the term ∂h_t/​∂h_(t​​-1) is less than 1, multiplying it repeatedly over many timesteps during backpropagation causes the gradient to diminish exponentially, which may approach zero and hence the term 'vanishing gradients'.

3.2: Exploding Gradients

On the flip side, if gradients are large (greater than one), they can increase exponentially during backpropagation. This leads to large updates to the weights, potentially causing the learning process to become unstable. The network may then produce outputs that are not numbers (NaN) or are infinitely large (infinity).

Exploding gradients occur when the gradients are greater than one, which can cause the gradients to grow exponentially:

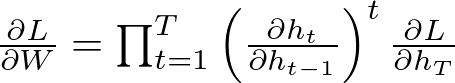
​If the term ​∂ht​_​/∂h_(t−1) is greater than 1 and is raised to the power of the timestep, it can become very large very quickly, especially for large values of t, leading to a situation where weight updates are too large, causing instability in the learning process.

3.3: Gradient Clipping

This technique limits the gradients during backpropagation to prevent them from becoming too large. By keeping the gradients within a defined range, it ensures that they don't cause the updates to become too extreme. Gradient clipping is easy to implement and has become standard practice in RNN training, effectively stabilizing the training process without major downsides.

Gradient clipping is a practical solution to mitigate the problem of exploding gradients. Mathematically, it can be applied as follows:

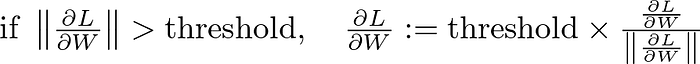
​​Here, ∥⋅∥ denotes the norm of the gradient, and the threshold is the maximum allowed value for the norm. If the gradient norm exceeds this threshold, it is scaled down to the threshold, preserving the direction of the gradient while limiting its magnitude

3.4: Adjusted Initialization Strategies

The initial setup of RNN weights is crucial. Methods like Glorot (Xavier) and He initialization help maintain an appropriate variance of activations and gradients as they pass through the network. These methods adjust the scale of initial weights based on the number of input and output neurons, promoting a more stable gradient flow across the network.

The Glorot (Xavier) initialization and He initialization set the scale of initial weights considering the size of the network layers:

Glorot (Xavier) Initialization

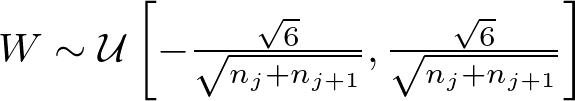
where n_j​ is the number of units in layer j and U represents a uniform distribution. This aims to keep the variance of activations constant for both forward and backward passes.

He Initialization

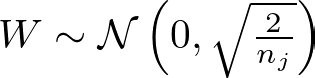
where W is the weight matrix initialized with values drawn from a normal distribution with mean 0 and variance 2/n_j​​, with n_j​ being the number of units in layer j. This initialization is particularly suited for layers with ReLU activations.

4: Building RNN from Scratch

For this demonstration, we will use the Air passenger dataset, which is a small open-source dataset hosted on GitHub.

Before diving into the code, I suggest you to keep this notebook on the side for a more comprehensive view of the code. This notebook contains all the code we will use in this implementation, feel free to run it and play with it!

Let's dive into the details of each component in the code to create a comprehensive guide on how this RNN is implemented from scratch!

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

We start by importing the necessary libraries. NumPy is essential for matrix operations which are fundamental to neural network computations. Pandas is used for data manipulation and analysis (particularly useful for handling time-series data in this case), and Matplotlib is for plotting (useful for visualizing training progress or model predictions).

4.1: Defining the RNN Class

class RNN:
    def __init__(self, input_size, hidden_size, output_size, init_method="random"):
        self.weights_ih, self.weights_hh, self.weights_ho = self.initialize_weights(input_size, hidden_size, output_size, init_method)
        self.bias_h = np.zeros((1, hidden_size))
        self.bias_o = np.zeros((1, output_size))
        self.hidden_size = hidden_size

    def initialize_weights(self, input_size, hidden_size, output_size, method):
        if method == "random":
            weights_ih = np.random.randn(input_size, hidden_size) * 0.01
            weights_hh = np.random.randn(hidden_size, hidden_size) * 0.01
            weights_ho = np.random.randn(hidden_size, output_size) * 0.01
        elif method == "xavier":
            weights_ih = np.random.randn(input_size, hidden_size) / np.sqrt(input_size / 2)
            weights_hh = np.random.randn(hidden_size, hidden_size) / np.sqrt(hidden_size / 2)
            weights_ho = np.random.randn(hidden_size, output_size) / np.sqrt(hidden_size / 2)
        elif method == "he":
            weights_ih = np.random.randn(input_size, hidden_size) * np.sqrt(2 / input_size)
            weights_hh = np.random.randn(hidden_size, hidden_size) * np.sqrt(2 / hidden_size)
            weights_ho = np.random.randn(hidden_size, output_size) * np.sqrt(2 / hidden_size)
        else:
            raise ValueError("Invalid initialization method")
        return weights_ih, weights_hh, weights_ho


    def forward(self, inputs):
        h = np.zeros((1, self.hidden_size))
        self.last_inputs = inputs
        self.last_hs = {0: h}

        for i, x in enumerate(inputs):
            x = x.reshape(1, -1)  # Ensure x is a row vector
            h = np.tanh(np.dot(x, self.weights_ih) + np.dot(h, self.weights_hh) + self.bias_h)
            self.last_hs[i + 1] = h

        y = np.dot(h, self.weights_ho) + self.bias_o
        self.last_outputs = y
        return y

    def backprop(self, d_y, learning_rate, clip_value=1):
        n = len(self.last_inputs)

        d_y_pred = (self.last_outputs - d_y) / d_y.size
        d_Whh = np.zeros_like(self.weights_hh)
        d_Wxh = np.zeros_like(self.weights_ih)
        d_Why = np.zeros_like(self.weights_ho)
        d_bh = np.zeros_like(self.bias_h)
        d_by = np.zeros_like(self.bias_o)
        d_h = np.dot(d_y_pred, self.weights_ho.T)

        for t in reversed(range(1, n + 1)):
            d_h_raw = (1 - self.last_hs[t] ** 2) * d_h
            d_bh += d_h_raw
            d_Whh += np.dot(self.last_hs[t - 1].T, d_h_raw)
            d_Wxh += np.dot(self.last_inputs[t - 1].reshape(1, -1).T, d_h_raw)
            d_h = np.dot(d_h_raw, self.weights_hh.T)

        for d in [d_Wxh, d_Whh, d_Why, d_bh, d_by]:
            np.clip(d, -clip_value, clip_value, out=d)
            
        self.weights_ih -= learning_rate * d_Wxh
        self.weights_hh -= learning_rate * d_Whh
        self.weights_ho -= learning_rate * d_Why
        self.bias_h -= learning_rate * d_bh
        self.bias_o -= learning_rate * d_by

This is the blueprint for our RNN. We will define the RNN's initialization, forward pass, and backpropagation within this class.

RNN Initialization

class RNN:
  def __init__(self, input_size, hidden_size, output_size, init_method="random"):
    self.weights_ih, self.weights_hh, self.weights_ho = self.initialize_weights(input_size, hidden_size, output_size, init_method)
    self.bias_h = np.zeros((1, hidden_size))
    self.bias_o = np.zeros((1, output_size))
    self.hidden_size = hidden_size

The __init__ method initializes the RNN with the number of neurons in each layer (input, hidden, output) and the method for weight initialization.

self.weights_ih, self.weights_hh, self.weights_ho = self.initialize_weights(input_size, hidden_size, output_size, init_method)

Here we call the initialize_weights method to set the weights according to the specified initialization method—'random', 'xavier', or 'he'. Each set of weights connects different layers of the network: weights_ih connects the input layer to the hidden layer, weights_hh connects the hidden layer to itself at the next timestep (capturing the 'recurrent' part of the RNN), and weights_ho connects the hidden layer to the output layer.

self.bias_h = np.zeros((1, hidden_size))
self.bias_o = np.zeros((1, output_size))

Biases are initialized to zero vectors, which will be adjusted during training. There's one bias for the hidden layer and one for the output layer.

Forward Pass Method

def forward(self, inputs):
    h = np.zeros((1, self.hidden_size))
    self.last_inputs = inputs
    self.last_hs = {0: h}
  
    for i, x in enumerate(inputs):
        x = x.reshape(1, -1)  # Ensure x is a row vector
        h = np.tanh(np.dot(x, self.weights_ih) + np.dot(h, self.weights_hh) + self.bias_h)
        self.last_hs[i + 1] = h
  
    y = np.dot(h, self.weights_ho) + self.bias_o
    self.last_outputs = y
    return y

The forward function takes a sequence of inputs and processes it through the RNN. It computes the hidden states and the final output in a loop over the sequence length.

h = np.zeros((1, self.hidden_size))

This initializes the hidden state as a vector of zeros. As the network sees more of the input sequence, this state will be updated to capture information from the inputs.

for i, x in enumerate(inputs):
    x = x.reshape(1, -1)  # Ensure x is a row vector
    h = np.tanh(np.dot(x, self.weights_ih) + np.dot(h, self.weights_hh) + self.bias_h)
    self.last_hs[i + 1] = h

For each input in the sequence, the code reshapes the input to ensure it's a row vector, then updates the hidden state using the current input, previous hidden state, weights, and biases. The np.tanh function introduces non-linearity necessary for complex pattern recognition.

y = np.dot(h, self.weights_ho) + self.bias_o

After processing the entire sequence, we compute the output using the last hidden state, the weights connecting the hidden layer to the output layer, and the output bias.

Backpropagation Through Time

def backprop(self, d_y, learning_rate, clip_value=1):
    n = len(self.last_inputs)
  
    d_y_pred = (self.last_outputs - d_y) / d_y.size
    d_Whh = np.zeros_like(self.weights_hh)
    d_Wxh = np.zeros_like(self.weights_ih)
    d_Why = np.zeros_like(self.weights_ho)
    d_bh = np.zeros_like(self.bias_h)
    d_by = np.zeros_like(self.bias_o)
    d_h = np.dot(d_y_pred, self.weights_ho.T)
  
    for t in reversed(range(1, n + 1)):
        d_h_raw = (1 - self.last_hs[t] ** 2) * d_h
        d_bh += d_h_raw
        d_Whh += np.dot(self.last_hs[t - 1].T, d_h_raw)
        d_Wxh += np.dot(self.last_inputs[t - 1].reshape(1, -1).T, d_h_raw)
        d_h = np.dot(d_h_raw, self.weights_hh.T)
  
    for d in [d_Wxh, d_Whh, d_Why, d_bh, d_by]:
        np.clip(d, -clip_value, clip_value, out=d)
        
    self.weights_ih -= learning_rate * d_Wxh
    self.weights_hh -= learning_rate * d_Whh
    self.weights_ho -= learning_rate * d_Why
    self.bias_h -= learning_rate * d_bh
    self.bias_o -= learning_rate * d_by

The backprop method implements the BPTT algorithm. It calculates gradients for each timestep and updates the weights and biases accordingly. Additionally, it incorporates gradient clipping by using np.clip to prevent the exploding gradients problem.

4.2: Early Stopping Mechanism

class EarlyStopping:
   def __init__(self, patience=7, verbose=False, delta=0):
        self.patience = patience
        self.verbose = verbose
        self.counter = 0
        self.best_score = None
        self.early_stop = False
        self.delta = delta

    def __call__(self, val_loss):
        score = -val_loss

        if self.best_score is None:
            self.best_score = score

        elif score < self.best_score + self.delta:
            self.counter += 1
            
            if self.counter >= self.patience:
                self.early_stop = True
        else:
            self.best_score = score
            self.counter = 0

This class provides an early stopping mechanism during training. If the validation loss hasn't improved after a certain number of epochs (patience), training is halted to prevent overfitting.

I won't dive into this class' explanation as I explained in details in this previous article:

4.3: RNN Trainer Class:

class RNNTrainer:
    def __init__(self, model, loss_func='mse'):
        self.model = model
        self.loss_func = loss_func
        self.train_loss = []
        self.val_loss = []

    def calculate_loss(self, y_true, y_pred):
        if self.loss_func == 'mse':
            return np.mean((y_pred - y_true)**2)
        
        elif self.loss_func == 'log_loss':
            return -np.mean(y_true*np.log(y_pred) + (1-y_true)*np.log(1-y_pred))
        
        elif self.loss_func == 'categorical_crossentropy':
            return -np.mean(y_true*np.log(y_pred))
        
        else:
            raise ValueError('Invalid loss function')

    def train(self, train_data, train_labels, val_data, val_labels, epochs, learning_rate, early_stopping=True, patience=10, clip_value=1):
        if early_stopping:
            early_stopping = EarlyStopping(patience=patience, verbose=True)
        for epoch in range(epochs):
            for X_train, y_train in zip(train_data, train_labels):
                outputs = self.model.forward(X_train)
                self.model.backprop(y_train, learning_rate, clip_value)
                train_loss = self.calculate_loss(y_train, outputs)
                self.train_loss.append(train_loss)

            val_loss_epoch = []
            for X_val, y_val in zip(val_data, val_labels):
                val_outputs = self.model.forward(X_val)
                val_loss = self.calculate_loss(y_val, val_outputs)
                val_loss_epoch.append(val_loss)

            val_loss = np.mean(val_loss_epoch)
            self.val_loss.append(val_loss)

            if early_stopping:
                early_stopping(val_loss)

                if early_stopping.early_stop:
                    print(f"Early stopping at epoch {epoch} | Best validation loss = {-early_stopping.best_score:.3f}")
                    break

            if epoch % 10 == 0:
                print(f'Epoch {epoch}: Train loss = {train_loss:.4f}, Validation loss = {val_loss:.4f}')

    def plot_gradients(self):
        for i, gradients in enumerate(zip(*self.gradients)):
            plt.plot(gradients, label=f'Neuron {i}')

        plt.xlabel('Time step')
        plt.ylabel('Gradient')
        plt.title('Gradients for each neuron over time')
        plt.legend()
        plt.show()

This class wraps the training process. It takes care of running the forward pass and backpropagation, computes the loss after each epoch, and maintains a history of training and validation losses.

Training Method

def train(self, train_data, train_labels, val_data, val_labels, epochs, learning_rate, early_stopping=True, patience=10, clip_value=1):
    if early_stopping:
        early_stopping = EarlyStopping(patience=patience, verbose=True)
    for epoch in range(epochs):
        for X_train, y_train in zip(train_data, train_labels):
            outputs = self.model.forward(X_train)
            self.model.backprop(y_train, learning_rate, clip_value)
            train_loss = self.calculate_loss(y_train, outputs)
            self.train_loss.append(train_loss)

        val_loss_epoch = []
        for X_val, y_val in zip(val_data, val_labels):
            val_outputs = self.model.forward(X_val)
            val_loss = self.calculate_loss(y_val, val_outputs)
            val_loss_epoch.append(val_loss)

        val_loss = np.mean(val_loss_epoch)
        self.val_loss.append(val_loss)

        if early_stopping:
            early_stopping(val_loss)

            if early_stopping.early_stop:
                print(f"Early stopping at epoch {epoch} | Best validation loss = {-early_stopping.best_score:.3f}")
                break

        if epoch % 10 == 0:
            print(f'Epoch {epoch}: Train loss = {train_loss:.4f}, Validation loss = {val_loss:.4f}')

Here we define the method that will train the RNN model. It loops over the specified number of epochs, processes the training data through the model, applies backpropagation, and tracks the training and validation losses.

4.4: Data Loading and Preprocessing

class TimeSeriesDataset:
    def __init__(self, url, look_back=1, train_size=0.67):
        self.url = url
        self.look_back = look_back
        self.train_size = train_size

    def load_data(self):
        df = pd.read_csv(self.url, usecols=[1])
        df = self.MinMaxScaler(df.values)  # Convert DataFrame to numpy array
        train_size = int(len(df) * self.train_size)
        train, test = df[0:train_size,:], df[train_size:len(df),:]
        return train, test
    
    def MinMaxScaler(self, data):
        numerator = data - np.min(data, 0)
        denominator = np.max(data, 0) - np.min(data, 0)
        return numerator / (denominator + 1e-7)

    def create_dataset(self, dataset):
        dataX, dataY = [], []
        for i in range(len(dataset)-self.look_back-1):
            a = dataset[i:(i+self.look_back), 0]
            dataX.append(a)
            dataY.append(dataset[i + self.look_back, 0])
        return np.array(dataX), np.array(dataY)

    def get_train_test(self):
        train, test = self.load_data()
        trainX, trainY = self.create_dataset(train)
        testX, testY = self.create_dataset(test)
        return trainX, trainY, testX, testY

This class handles the loading, preprocessing, and batching of time-series data. It is designed to facilitate the handling of data that will be fed into the RNN.

def load_data(self):
        df = pd.read_csv(self.url, usecols=[1])
        df = self.MinMaxScaler(df.values)  # Convert DataFrame to numpy array
        train_size = int(len(df) * self.train_size)
        train, test = df[0:train_size,:], df[train_size:len(df),:]
        return train, test

This method loads data from a CSV file specified by a URL. It uses Pandas to handle the CSV and extracts the necessary columns.

def MinMaxScaler(self, data):
    numerator = data - np.min(data, 0)
    denominator = np.max(data, 0) - np.min(data, 0)
    return numerator / (denominator + 1e-7)

This is a normalization function that scales the data between 0 and 1. This is a common practice in time series and other types of data processing to help neural networks learn more effectively.

def create_dataset(self, dataset):
    dataX, dataY = [], []
    for i in range(len(dataset)-self.look_back-1):
        a = dataset[i:(i+self.look_back), 0]
        dataX.append(a)
        dataY.append(dataset[i + self.look_back, 0])
    return np.array(dataX), np.array(dataY)

It reformats the loaded data into a suitable format where dataX contains input sequences for the model and dataY contains the corresponding labels or targets for each sequence.

def get_train_test(self):
    train, test = self.load_data()
    trainX, trainY = self.create_dataset(train)
    testX, testY = self.create_dataset(test)
    return trainX, trainY, testX, testY

This splits the loaded data into training and testing datasets based on a specified proportion.

Loading and Preparing the Data

url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/daily-min-temperatures.csv'
dataset = TimeSeriesDataset(url, look_back=1)
trainX, trainY, testX, testY = dataset.get_train_test()

Here, we specify the URL of the dataset, instantiate the TimeSeriesDataset with a look_back of 1, which means each input sequence (used for training the RNN) will consist of 1 timestep. The data is then split into training and testing sets.

trainX = np.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1]))
testX = np.reshape(testX, (testX.shape[0], 1, testX.shape[1]))

The input data needs to be reshaped to fit the RNN input requirements, which generally expect data in the format of [samples, time steps, features].

4.5: Training the RNN

rnn = RNN(look_back, 256, 1, init_method='xavier')
trainer = RNNTrainer(rnn, 'mse')
trainer.train(trainX, trainY, testX, testY, epochs=100, learning_rate=0.01, early_stopping=True, patience=10, clip_value=1)

The RNN model is instantiated with Xavier initialization, and then it is trained using the RNNTrainer. The trainer uses Mean Squared Error ('mse') as the loss function, which is suitable for regression tasks like time-series forecasting.

This implementation covers all the basic components needed to set up, train, and use an RNN for a simple time-series prediction task. The code structure facilitates understanding and modification for more complex or different types of sequence modeling tasks.

5: Advanced RNN Architectures

5.1: Long Short-Term Memory Networks (LSTMs)

LSTMs are a type of RNN architecture built to address the limitations of traditional RNNs, especially the vanishing gradient problem. They feature a unique internal structure that significantly enhances their ability to process sequences.

LSTMs have a dedicated memory cell that can store information for extended periods. Their effectiveness comes from the gate mechanisms they utilize: the input gate, forget gate, and output gate. These gates control the information flow, determining what to retain or remove from memory and what to output at each step. This gated system allows for precise updates to the memory cell, either adding or deleting information as needed.

Thanks to these gating mechanisms, LSTMs excel at managing long-term dependencies, making them suitable for tasks like language modeling, where the context from earlier in the text influences comprehension or predictions. They are also adept at time-series prediction, where past information is critical in forecasting future events.

5.2: Gated Recurrent Units (GRUs)

GRUs are a streamlined variant of RNNs that modify the LSTM design to achieve similar results with less complexity. They are noted for their efficiency

GRUs merge the input and forget gates into a single "update gate" and combine the cell state and hidden state. This simpler structure reduces the model's complexity, which can lead to quicker computations and lower memory usage — benefits that are particularly valuable when computational resources are limited.

GRUs are often favored over LSTMs for smaller datasets where LSTMs might overfit due to their complexity, or when faster training is essential. They perform well on many tasks that don't involve very long-term dependencies.

5.3: Bidirectional RNNs

Bidirectional RNNs (Bi-RNNs) enhance traditional RNNs by processing data in both forward and backward directions simultaneously.

In a Bi-RNN, each sequence is fed through two separate recurrent layers — one forwards and one backward — both linked to the same output layer. This setup enables the network to learn from both past and future contexts at once, improving the model's ability to utilize available information throughout the sequence.

This bidirectional approach is particularly useful in tasks where understanding the full context is crucial, such as in speech recognition, where it helps interpret speech by considering both preceding and subsequent sounds, or in text translation, where comprehending entire sentences before translating can enhance accuracy.

These advanced RNN architectures incorporate structural innovations that improve their ability to capture temporal dependencies and offer robust solutions across a broad range of sequence modeling tasks. Their capacity to maintain context over time and learn from sequences in multiple directions makes them invaluable tools for machine learning practitioners.

6: Conclusion

In this article, we've taken a close look at Recurrent Neural Networks (RNNs), focusing on what makes them tick, the challenges they face during training, and some sophisticated designs that boost their effectiveness. Here's a breakdown:

We examined the structure of RNNs, highlighting their unique capability to process sequences thanks to their internal memory states. We covered essential processes like the forward pass and backpropagation through time (BPTT), explaining how these processes are tailored for handling sequences.

Finally, we pointed out major hurdles such as the vanishing and exploding gradient problems that can derail training. We discussed solutions like gradient clipping and specific initialization strategies that help stabilize the training process and enhance the network's ability to learn from longer sequences.

References

• Brownlee, J. Daily Minimum Temperatures Dataset. Retrieved from https://raw.githubusercontent.com/jbrownlee/Datasets/master/daily-min-temperatures.csv
• Towards Data Science. (n.d.). The Math Behind Fine-Tuning Deep Neural Networks. Retrieved from https://medium.com/towards-data-science/the-math-behind-fine-tuning-deep-neural-networks-8138d548da69
• Towards Data Science. (n.d.). The Math Behind Deep CNN — AlexNet. Retrieved from https://medium.com/towards-data-science/the-math-behind-deep-cnn-alexnet-738d858e5a2f
• Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.

You've reached the end — well done! I hope you found this article insightful. If you liked it, please consider giving it a thumbs up and following for more content like this. I aim to demystify machine learning by recreating popular algorithms from the ground up and making them accessible to everyone. Stay tuned for more updates!