Gödel, Escher, Bach: An Eternal Golden Braid (henceforth: GEB), the Pulitzer Prize winning book written in 1978 by Douglas Hofstadter, is described in its cryptic tagline as "a metaphorical fugue on minds and machines in the spirit of Lewis Carroll."
I recently reread GEB and got fired up by how brilliantly Hofstadter fuses computation, epistemology, and consciousness. After failed attempts at explaining the book to three of my smartest friends, I decided to write something up.
The problem is that a simple reduction like "GEB is about how complex systems arise from simpler systems" is akin to describing Ulysses as "a day in the life of Leopold Bloom." More detailed descriptions run the risk of diving into the depth that's only understandable after having read the book.
This post is a more modest attempt to explain to myself why GEB is important, and focuses on three mental models that have profoundly affected my life: epistemic limits, self-reference, and isomorphism.
If it causes you to read or reread it, then all the better.
Here we go!
The main character of the book is Kurt Gödel, the most important person in the 20th century you've never heard of. Gödel is the kind of guy that shows up to his buddy's 70th birthday with an exact solution to the Einstein field equations as a present. Despite being the greatest mathematician of his generation, he wasn't stuffy in the least: his favorite movie was Snow White and the Seven Dwarves.
Gödel is most famous for his Incompleteness Theorems, which established limits on mathematics. For the first chunk of the 20th century, mathematicians were obsessed with formalizing mathematics and then proving meta-theorems about those formal systems. In particular, there was a strongly-held belief that for any well-formed formula (a "grammatically correct" statement in math, e.g., A=B is well-formed whereas AA==+B is not), you could use mathematics to decide whether it was true or false.
If you think about it for a second, this makes perfect sense: it seems like you should be able to determine whether any statement is true or false.
Nope! Gödel proved in 1931 that mathematics is not decidable, an earth-shattering result. He proved that there are statements in mathematics, which are true but not provable within the system. Worse yet, it turns out that you can't build a more powerful mathematical system. Once a system becomes sufficiently complex, there will always be statements which are undecidable. You're left with a choice: either have weak system of mathematics or accept that there will always be theorems out of reach. A rough analogy to incompleteness Heisenberg's Uncertainty Principle, which shows that physics makes it impossible to determine both the position and velocity of a particle with exact precision.
Wouldn't it be nice if every question had an answer? That's a lovely fantasy, but Gödel shows that there are fundamental epistemic limits to the universe, things that no genius will help us to know, no alien race could teach us, no machine could be built to solve, and no new kinds of mathematics will uncover. How frustrating.
A key feature of powerful mathematical systems (or perhaps, any system that generates complexity…) is that they involve self-reference, that is, they contain ways of talking about themselves. "This sentence is true" is an example. Because self-referential systems can manipulate and talk about themselves, they systems are very powerful and immediately run into fun paradoxes. Is the statement "This sentence is false." true or false? Either way, it doesn't end well.
A third major theme of the book is isomorphism, which is unique to Hofstadter's vernacular. In formal mathematics, "isomorphism" takes on a version of "equivalence." For example, it turns out that many different formalizations of mathematics are provably isomorphic, like Turing Machines, arithmetic, set theory, and formal logic. Hofstadter deliberately uses the term more loosely to describe two systems that are structurally similar. I find this quite useful because it forces one to define the structures of the system, why they are similar, and why other parts of the system are less important. We might describe the way that planets fly around stars as isomorphic to the way that electrons fly around nuclei.
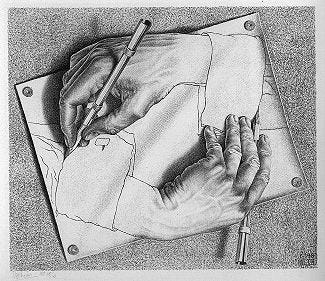
The two minor characters, M.C.Escher and Johann Sebastian Bach, are reflections of Gödel in art and both liberally use self reference. Escher draws pictures of hands drawing hands (!) and water "falling" in an infinite loop. His images don't just play tricks on the eye, they force paradoxical conclusions, regardless of your angle of interpretation. On the musical side, Papa Bach was most famous for his complex fugues, which are basically the same melody played on top of each other. Common versions of this you might have sung as a child are "Row, row, row your boat" and "Frère Jacques." Both Escher and Bach are woven into the story (like a fugue?), providing tangible examples to the more abstruse mathematical concepts.
Perhaps the most astonishing part of the book is the quality of the writing itself. Each chapter begins with a clever dialog between Achilles and the Tortoise (inspired by Lewis Carroll), and a few of their anthropomorphic friends. They deal with a whole range of bizarre situations, like record player so powerful that it can play any record (including a record that can destroy the record player) and asking a Djinn for a meta-wish ("I wish for 5 more wishes"). Hofstadter's greatest achievement is his palindromic Crab Canon in Chapter VII, which is a dialog that can be read backwards and forwards. Of course, these aren't just cute dialogs: each is isomorphic to the themes in the following chapter. Oftentimes a dialog is a more understandable exposition of the chapter's theme than the chapter itself.
And, naturally in a book about self-reference, GEB itself is highly self-referential. Themes are often resolved hundreds of pages later and require going back to appreciate fully the depth of Hofstadter's argument. Mercifully, he's a gifted and lucid writer so, even though there are chapters that are dense, it's always tractable to read.
After 742 pages and even after having written the paragraphs above, I still struggle with a simple answer to the question: "What is this book about?" The best I can come up with is that GEB equips you with mental models to contemplate philosophy.
So to end, a few personal examples about how GEB has influenced my own thinking.
I recently joined Stand Together, who shares my strong belief in bottom up solutions. Perhaps the idea that bottom up solutions are better isn't just an empirical statement of sociology, but fundamental to the nature of complex systems. Indeed, Hofstadter goes through many examples of how complexity emerges from simpler systems, often which look nothing like the higher-level systems. Consciousness itself doesn't exist in neurons, and yet neurons as a system create consciousness in humans (this is critical to Hoftstadter's argument that machines can think). There's also a fantastical example in a dialog with the Anteater, who has conversations with Aunt Hilary, an ant colony. She is perfectly capable of having a robust conversation with the Anteater, powered by the ants in the colony. Of course, the ants themselves are individuals with their own cares and concerns and has no knowledge of the emergent intelligence, much like Aunt Hilary has no knowledge of her inner workings.
How DNA expresses as proteins, how the brain functions at multiple levels, how we understand and use words, how programs don't have access to the underlying transistors, how Aunt Hilary doesn't know what the ants are doing… all of these are a set of isomorphisms that suggest that bottom up is better than top down. An additional tenet of Stand Together is "believe in people," which means that the smallest units act intelligently. Like ants or neurons, we make local decisions every day that bubble up into the structure of society, without anyone telling us what to do.
The idea that epistemic limits exist in something as universal as mathematics has humbled me about the limits of knowledge for complex human systems. Utopian thought experiments often generate useful frames of exploration, but ought not be confused with reality. Utopians often try to pull out the "bugs" from human systems, often which are endemic to the system, or "features," as we might say in the trade. Bugs might not be desirable, but sometimes, the bugs can't just be ripped out of the system without destroying the system itself. Our time would be better spent figuring out—within the system—optimize for minimizing the downsides of the "bugs" while maximizing the value of the features. Think about this with respect to capitalism, socialism, and communism…
A final area where GEB has influenced me is in designing software products. Hugh Dubberly has been my collaborator for years, starting off with our deep dive into cybernetics, the study of feedback loops. We believe that iteration is key to quality; perfection is impossible out of the gate. Further, the system used to generate quality software is a series of feedback loops between customers and the company, product and engineering, and so on. Though specific product frameworks have changed over the years, that obsession with iteration and feedback permeates everything I've implemented.
My modest goal in writing this post was to have something I could send to a friend, rather than to spend an hour fumbling a feeble explanation of Gödel, Escher, Bach. I had a secondary goal in the back of my head… if you have a copy of GEB on your shelf collecting dust and you've never read more than a chapter or two, dust it off and see how it goes this time.
