Introduction

Imagine you're trying to predict stock prices, but instead of just guessing whether the price will go up or down tomorrow, you're asking a smarter question: What happens if tomorrow's price crosses a certain threshold? For instance, if a stock price drops below a key support level, what's likely to happen in the following days? This kind of conditional forecasting is not only more insightful but also mirrors real-world decisions made in financial markets.

The problem is that traditional time series models aren't built for these "what if" scenarios. That's where Markov Decision Theory meets neural state space models like Mamba to create something new. By extending the classic state space framework, we can bake future conditions — like "tomorrow's price event" — directly into the prediction process. Think of it as giving the model a crystal ball, allowing it to consider not just the past but also what might happen next.

In this new approach, we explore how adding event-driven dynamics to Mamba state space models unlocks exciting possibilities for forecasting. We connect these ideas to Markov Decision Processes (MDPs) to show why they're so useful for complex, high-stakes predictions like stock price movements. With simple examples, clear equations, and real-world data, we'll demonstrate just how powerful and practical this method can be.

Event-Driven Prediction: Expanding Mamba State Space Models for Conditional Forecasting

Background and Mechanism

The presented approach is a novel extension of the Mamba State Space Neural Network (NN) framework for conditional time-series forecasting, tailored to predict stock price movements under specific events. Unlike traditional forecasting methods that focus on directly predicting future values, this method forecasts the conditional distribution P(future price ∣ past price, event), where the event (e.g., a price drop below a threshold) influences future trajectories:

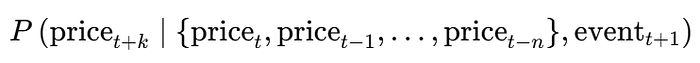
Here:

• price_{t+k}​: The future price k-steps ahead we aim to predict.
• {price_t, pricet_1,…,price_tn}: The past n-time steps of historical prices.
• event_{t+1}​: The triggering event (e.g., price falling below a moving average) that occurs at time t+1.

This means I try to capture the conditional distribution of the future price given the historical price sequence and the occurrence of an event.

This idea comes from combining inspiration from Markov Decision Theory (MDP) and neural state space modeling. The goal is to make predictions more accurate and easier to interpret, especially in financial markets where decisions often depend on specific events.

Below, I analyze the key components and their integration:

Conditional Prediction via State-Space Representation

The forecasting goal is to estimate the dynamic behavior of stock prices given historical data and an event trigger.

The dynamic system is represented as:

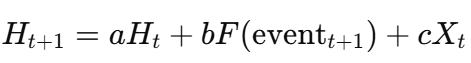
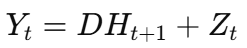
Here:

• H_t: The hidden state at time t, capturing past dynamics.
• F(event_t + 1): A function modeling the impact of future events (e.g., price breaking a support line) on state transitions.
• X_t​: Explanatory variables such as price, volume, and volatility.
• a, b, c: Trainable parameters modeling state transition dynamics.
• Y_t​: The observed output (e.g., binary prediction of a price increase).

From the expressions above, it's clear that this conditional forecasting system is closely tied to Markov Decision Processes (MDP) and the Mamba State Space Neural Network (NN) framework. This means we can build on MDP and Mamba to handle conditional multiple time series forecasting.

Connection to Markov Decision Theory

This system closely relates to Markov Decision Theory (MDP) framework:

Markov Decision Theory (MDP): In MDP, we define states, actions, and state transitions. Here:

• The state (S_t​) represents the historical prices and features.
• The action (A_t​) is whether the event (e.g., price drop) occurs.
• The state transition is the conditional forecasting process:

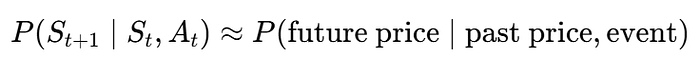
In the context of this system, MDP maps directly to the forecasting problem:

State (S_t):

Includes historical stock data like prices, trading volume, and volatility. For example:

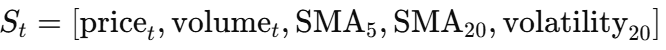
Action (A_t​):

Represents whether an event, such as a price drop, occurs. For example:

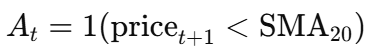
State Transition:

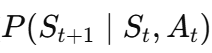
The transition models how the system evolves based on the event. For example, if the price drops below the moving average (A_t = 1), the model predicts the likelihood of a price rebound.

Reward (R_t​):

It can represent the trader's profit or loss based on the action taken. For instance:

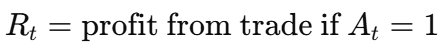
Policy (π(S_t​)):

This defines the optimal strategy for trading decisions. For example, Take action A_t = 1 if the model predicts a price rebound with probability:

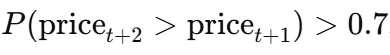
Here's why MDP is so useful in this system:

Handles Uncertainty: It captures the randomness and uncertainty of how the market behaves.

Event-Based Predictions: It provides forecasts that are tied to specific events, like price drops, which follows how traders think and make decisions.

Adapts Dynamically: It learns how events influence future market behavior, making its predictions more accurate and relevant.

By connecting MDP, this approach may bridge the gap between decision theory and practical financial forecasting.

Extending Mamba State Space Models for Conditional Time-Series Forecasting

How Do Mamba State Space Models Predict Multiple Time-Series?

The Mamba State Space Model (SSM) is a neural network framework designed to efficiently model multiple time-series forecasting by leveraging state-space representations. Unlike standard deep learning architectures, Mamba is structured to capture long-range dependencies in sequential data using hidden states that evolve dynamically over time.

A standard Mamba state-space model follows the state update equation:

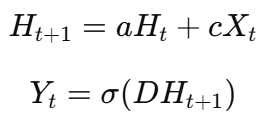
or with activation function way:

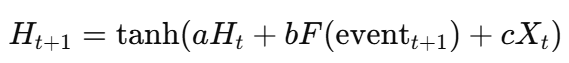
where:

• H_t represents the hidden state at time t, encoding historical information.
• a is a trainable transition matrix that controls how the hidden state evolves over time.
• cX_t​ captures external input features, such as lagged variables, seasonality, or exogenous factors.
• Y_t​ is the model's prediction, often passed through an activation function σ (e.g., sigmoid for binary classification or identity for regression).
• D is a transformation matrix that maps hidden states to observable outputs.

This formulation is highly flexible, making it suitable for multi-variate time-series forecasting, where the hidden state acts as a nonlinear transformation of autoregressive components.

Let me interpret Hidden States in Mamba SSM:

The hidden state H_t​ in Mamba can be viewed as a learned nonlinear transformation of lagged variables and seasonal components. In classical time-series models like ARMA or VAR, the future value of Y_t​ is modeled as a weighted sum of past observations and external covariates. However, Mamba generalizes this by learning an encoded representation of these dependencies:

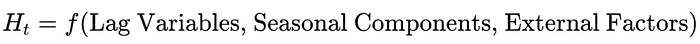
where f(⋅) is a learned function through the state-space neural network. This allows Mamba to:

1. Capture nonlinear relationships between historical patterns.
2. Adaptively encode multi-scale dependencies, improving forecasting accuracy.
3. Efficiently handle multi-series dependencies, making it ideal for stock price modeling.

Extending Mamba: Introducing Dynamic Event Nodes for Conditional Forecasting:

A key limitation of traditional Mamba models is that they only model time-series transitions passively, without explicit conditioning on external dynamic events (e.g., major price movements, economic shocks).

We propose an extension of Mamba SSM by adding a dynamic event node to the hidden layer, making it event-driven:

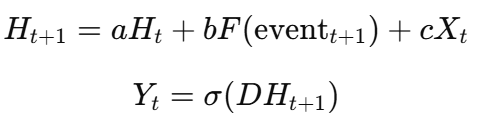
where:

• F(event_{t+1}) is a function modeling the influence of future event triggers (e.g., price crossing a moving average, volatility spike).
• The additional term bF(event_{t+1}) dynamically modifies the hidden state, allowing the model to adjust forecasts based on predicted external shocks.

This results in a conditional time-series forecasting model, where predictions depend not only on past prices but also on whether specific future conditions occur.

Algorithm Steps

Feature Engineering: Extract features such as moving averages, volatility, and event triggers:

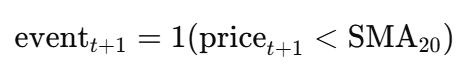
State-Space Initialization: Initialize hidden states H_t​ and trainable parameters a, b, c.

Training: Optimize model parameters by minimizing a loss function (e.g., Binary Cross-Entropy Loss for classification).

Evaluation: Compute metrics such as AUC, F1 Score, and KS Statistic to assess performance.

Example: Why This Extension is Important for Stock Price Prediction

Suppose we have 500 days of stock data for AAPL, including price and volume. The task is to predict whether the stock price will increase by at least 1% tomorrow if today's price falls below the 20-day moving average.

• Event: event_{t+1} = (price_{t+1} < SMA20)
• Features: X_t = [price, volume, SMA5, SMA20, volatility20]
• Prediction: P(price increase ∣ X_t, event_{t+1})

The model incorporates these components to make event-driven predictions:

1. If the event occurs (e.g., price drops below the SMA), the model predicts a 70% probability of a price increase the next day.
2. Traders can act based on this probability, e.g., buying shares when the event indicates bullish potential.

Moving Beyond ARMA Models

Traditional models like ARMA/ARIMA have notable limitations in multi-time-series forecasting. They require individual modeling for each stock, making it difficult to capture inter-stock dependencies such as price co-movements within sectors. These models primarily rely on univariate data (e.g., price history), leaving out valuable features like volume, technical indicators, or market events, which are essential for modern financial forecasting.

In contrast, Extended State Space Neural Networks (SSM) offer a unified framework to model multiple stocks simultaneously. By introducing a shared hidden state H(t), the model learns common patterns (e.g., market-wide trends) while capturing unique dynamics for individual stocks. This approach enables the use of global features, such as market-wide volatility or correlations between stock returns, alongside stock-specific data like price and volume.

The inclusion of event-driven mechanisms, F(event_tomorrow), further enhances the model's ability to predict market behavior under specific conditions. For example, if a stock breaks a support line, the event's impact on related stocks can be captured and propagated through the network. This allows the model to efficiently utilize all stocks' data and predict the ripple effects of key events across the market.

Unified models like these are data-efficient and scalable. Instead of training 100 separate models for 100 stocks, a single state-space neural network can leverage the entire dataset to deliver more accurate and coherent forecasts, making it a superior choice for modern financial applications.

Data and Code Experiment

This experiment extends the Mamba State Space Model (SSM) for event-driven multi-time-series forecasting in financial markets, exploring both continuous and binary target predictions.

The continuous target model estimates future stock prices based on historical trends and market events, using SMA (5, 20-day), volatility, and volume as predictors. It is evaluated with RMSE and MAPE, providing estimated price levels under specific conditions.

This paper focuses on the theoretical novelty of the approach rather than a full-scale implementation. At this stage, simple simulated data is used to demonstrate feasibility. Future work will integrate real financial data, explore alternative economic indicators, refine event definitions, and enhance model robustness. This framework has significant potential, and I encourage further research and adaptation to advance event-driven financial forecasting.

################Model 1: Continuous Target###########################    
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, Dataset
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import TimeSeriesSplit
from sklearn.metrics import roc_auc_score, f1_score, roc_curve

# Load Data from CSV
DF = pd.read_csv("stocks.csv")

# Feature Engineering
def feature_engineering(df):
    df = df.copy()  # Work on a copy
    df["SMA_5"] = df.groupby("ticker")["price"].transform(lambda x: x.rolling(window=5).mean())
    df["SMA_20"] = df.groupby("ticker")["price"].transform(lambda x: x.rolling(window=20).mean())
    df["volatility_20"] = df.groupby("ticker")["price"].transform(lambda x: x.rolling(window=20).std())
    df["event_tomorrow"] = (df["price"] < df["SMA_20"]).astype(int)  # Binary event

    # Replace NaN values
    df.fillna(0, inplace=True)

    # Ensure all relevant columns are numeric
    numeric_columns = ["price", "volume", "SMA_5", "SMA_20", "volatility_20", "event_tomorrow"]
    for col in numeric_columns:
        df[col] = pd.to_numeric(df[col], errors="coerce").astype(np.float32)

    return df

# Dataset Class
class StockDataset(Dataset):
    def __init__(self, data):
        numeric_columns = ["price", "volume", "SMA_5", "SMA_20", "volatility_20", "event_tomorrow"]
        self.data = data[numeric_columns].copy()  # Ensure only numeric columns are used

        # Initialize scaler and scale features
        self.scaler = StandardScaler()
        self.features = numeric_columns  # Features used in the model
        scaled_features = self.scaler.fit_transform(self.data[self.features].values)
        self.data.loc[:, self.features] = scaled_features.astype(np.float32)

    def __len__(self):
        return len(self.data)

    def __getitem__(self, idx):
        # Fetch the row at the given index
        row = self.data.iloc[idx]

        # Extract features (x) and target (y)
        x = row[self.features].values
        y = row["price"]

        # Convert to PyTorch tensors
        x = torch.tensor(x, dtype=torch.float32)
        y = torch.tensor(y, dtype=torch.float32)
        return x, y

# Updated MambaExtendedNN with Dropout and Regularization
class MambaExtendedNN(nn.Module):
    def __init__(self, input_dim, hidden_dim):
        super(MambaExtendedNN, self).__init__()
        self.hidden_dim = hidden_dim
        self.a = nn.Parameter(torch.rand(hidden_dim, hidden_dim))  # Transition matrix for state
        self.b = nn.Parameter(torch.rand(1, hidden_dim))  # Event effect
        self.c = nn.Linear(input_dim, hidden_dim)  # Input transformation
        self.dropout = nn.Dropout(0.2)  # Dropout for regularization
        self.fc_output = nn.Linear(hidden_dim, 1)  # Output layer
        self.log_var = nn.Parameter(torch.zeros(1))  # Log variance for uncertainty

    def forward(self, x, h, event):
        event_effect = self.b * event.unsqueeze(1)
        a_expanded = self.a.unsqueeze(0).expand(x.size(0), -1, -1)
        h_next = torch.bmm(h.unsqueeze(1), a_expanded).squeeze(1)
        h_next = h_next + event_effect + self.c(x)
        h_next = self.dropout(h_next)  # Apply dropout
        y_pred = self.fc_output(h_next)
        return y_pred, h_next, self.log_var


# Training Function with MAPE Calculation
def train_model(model, dataloader, optimizer, criterion, num_epochs):
    for epoch in range(num_epochs):
        model.train()
        total_loss = 0
        for x, y in dataloader:
            optimizer.zero_grad()
            batch_size = x.size(0)
            h = torch.zeros((batch_size, model.hidden_dim), dtype=torch.float32)
            event = x[:, -1]
            x = x[:, :-1]
            y_pred, h, log_var = model(x, h, event)
            loss = criterion(y_pred.squeeze(), y)
            loss.backward()
            optimizer.step()
            total_loss += loss.item()
        print(f"Epoch {epoch + 1}/{num_epochs}, Loss: {total_loss / len(dataloader):.4f}")


# Evaluation Function with MAPE
def evaluate_model(model, dataloader):
    model.eval()
    predictions, actuals = [], []
    mape_total, count = 0, 0
    with torch.no_grad():
        for x, y in dataloader:
            batch_size = x.size(0)
            h = torch.zeros((batch_size, model.hidden_dim), dtype=torch.float32)
            event = x[:, -1]
            x = x[:, :-1]
            y_pred, h, log_var = model(x, h, event)
            predictions.extend(y_pred.squeeze().tolist())
            actuals.extend(y.tolist())
            # Calculate MAPE
            mape_total += torch.sum(torch.abs((y_pred.squeeze() - y) / y)).item()
            count += len(y)
    mape = (mape_total / count) * 100
    return predictions, actuals, mape


# Updated Time Series Split and Evaluation Loop
results = []
for train_idx, test_idx in ts_split.split(all_data):
    train_data, test_data = all_data.iloc[train_idx].copy(), all_data.iloc[test_idx].copy()

    train_data = feature_engineering(train_data)
    test_data = feature_engineering(test_data)

    train_dataset = StockDataset(train_data)
    test_dataset = StockDataset(test_data)

    train_loader = DataLoader(train_dataset, batch_size=32, shuffle=False)
    test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)

    model = MambaExtendedNN(input_dim=5, hidden_dim=10)
    optimizer = optim.AdamW(model.parameters(), lr=0.0005, weight_decay=1e-4)  # Added L2 regularization
    criterion = nn.MSELoss()

    print("Training Model...")
    train_model(model, train_loader, optimizer, criterion, num_epochs=100)

    print("Evaluating Model...")
    predictions, actuals, mape = evaluate_model(model, test_loader)
    results.append((predictions, actuals, mape))

# Analyze and Print Results
for i, (pred, actual, mape) in enumerate(results):
    mse = np.mean((np.array(pred) - np.array(actual)) ** 2)
    print(f"Fold {i + 1}, MSE: {mse:.4f}, MAPE: {mape:.2f}%")
    print("Explanation for Traders:")
    print(
        f"In Fold {i + 1}, the model predicts stock price movements with an average error of {mape:.2f}%."
        " If the predicted price for a stock (e.g., AAPL) is $180 under conditions of high volatility, "
        "this suggests a potential mean price level traders can expect based on recent trends."
    )

#################Results##########################
.....
Epoch 93/100, Loss: 0.0396
Epoch 94/100, Loss: 0.0496
Epoch 95/100, Loss: 0.0417
Epoch 96/100, Loss: 0.0444
Epoch 97/100, Loss: 0.0365
Epoch 98/100, Loss: 0.0415
Epoch 99/100, Loss: 0.0413
Epoch 100/100, Loss: 0.0435

Evaluating Model...
Fold 1, MSE: 0.0935, MAPE: 46.80%
Explanation for Traders:
In Fold 1, the model predicts stock price movements with an average error of 46.80%. If the predicted price for a stock (e.g., AAPL) is $180 under conditions of high volatility, this suggests a potential mean price level traders can expect based on recent trends.
Fold 2, MSE: 0.0164, MAPE: 46.75%
Explanation for Traders:
In Fold 2, the model predicts stock price movements with an average error of 46.75%. If the predicted price for a stock (e.g., AAPL) is $180 under conditions of high volatility, this suggests a potential mean price level traders can expect based on recent trends.
Fold 3, MSE: 0.0165, MAPE: 32.97%
Explanation for Traders:
In Fold 3, the model predicts stock price movements with an average error of 32.97%. If the predicted price for a stock (e.g., AAPL) is $180 under conditions of high volatility, this suggests a potential mean price level traders can expect based on recent trends.
Fold 4, MSE: 0.0108, MAPE: 14.42%
Explanation for Traders:
In Fold 4, the model predicts stock price movements with an average error of 14.42%. If the predicted price for a stock (e.g., AAPL) is $180 under conditions of high volatility, this suggests a potential mean price level traders can expect based on recent trends.
Fold 5, MSE: 0.0018, MAPE: 4.79%
Explanation for Traders:
In Fold 5, the model predicts stock price movements with an average error of 4.79%. If the predicted price for a stock (e.g., AAPL) is $180 under conditions of high volatility, this suggests a potential mean price level traders can expect based on recent trends.

The binary target model below predicts whether a stock's price will rise by at least 1%, incorporating a dynamic event-driven node to enhance conditional forecasting. It is validated using AUC, F1 Score, and KS Statistic, offering probability-based insights for event-driven trading decisions.

#################Model 2: Binary target###########################    

def feature_engineering(df, prediction_horizon=5):
    df = df.copy()

    # Calculate moving averages, volatility, and the future price
    df["SMA_5"] = df.groupby("ticker")["price"].transform(lambda x: x.rolling(window=5).mean())
    df["SMA_20"] = df.groupby("ticker")["price"].transform(lambda x: x.rolling(window=20).mean())
    df["volatility_20"] = df.groupby("ticker")["price"].transform(lambda x: x.rolling(window=20).std())
    df["future_price"] = df.groupby("ticker")["price"].shift(-prediction_horizon)

    # Binary target: Price increase ≥ 1%
    df["binary_target"] = (df["future_price"] / df["price"] - 1 >= 0.01).astype(int)

    # Replace NaN values in numeric columns with 0
    numeric_columns = ["price", "volume", "SMA_5", "SMA_20", "volatility_20", "binary_target"]
    df[numeric_columns] = df[numeric_columns].fillna(0)

    # Drop non-numeric columns like 'ticker' and 'date' if present
    df = df[numeric_columns]

    # Convert all columns to float32 for compatibility with PyTorch
    df = df.astype(np.float32)

    return df

# Dataset Class
class StockDataset(Dataset):
    def __init__(self, data):
        # List of numeric features used for training
        numeric_columns = ["price", "volume", "SMA_5", "SMA_20", "volatility_20"]
        self.data = data.copy()
        self.features = numeric_columns

        # Standardize the numeric features
        self.scaler = StandardScaler()
        scaled_features = self.scaler.fit_transform(self.data[self.features].values)
        self.data.loc[:, self.features] = scaled_features.astype(np.float32)

    def __len__(self):
        return len(self.data)

    def __getitem__(self, idx):
        # Extract features (x) and binary target (y)
        row = self.data.iloc[idx]
        x = row[self.features].values
        y = row["binary_target"]
        return torch.tensor(x, dtype=torch.float32), torch.tensor(y, dtype=torch.float32)

# Extended Mamba Neural Network
class MambaExtendedNN(nn.Module):
    def __init__(self, input_dim, hidden_dim):
        super(MambaExtendedNN, self).__init__()
        self.hidden_dim = hidden_dim
        self.a = nn.Parameter(torch.rand(hidden_dim, hidden_dim))  # Transition matrix for state
        self.b = nn.Parameter(torch.rand(1, hidden_dim))  # Event effect
        self.c = nn.Linear(input_dim, hidden_dim)  # Input transformation
        self.dropout = nn.Dropout(0.2)
        self.fc_output = nn.Sequential(nn.Linear(hidden_dim, 1), nn.Sigmoid())  # Binary classification output

    def forward(self, x, h, event):
        event_effect = self.b * event.unsqueeze(1)
        a_expanded = self.a.unsqueeze(0).expand(x.size(0), -1, -1)
        h_next = torch.bmm(h.unsqueeze(1), a_expanded).squeeze(1)
        h_next = h_next + event_effect + self.c(x)  # Ensure x has correct dimensions
        h_next = self.dropout(h_next)
        y_pred = self.fc_output(h_next)
        return y_pred, h_next

def train_model(model, dataloader, optimizer, criterion, num_epochs):
    for epoch in range(num_epochs):
        model.train()
        total_loss = 0
        for x, y in dataloader:
            optimizer.zero_grad()
            batch_size = x.size(0)
            h = torch.zeros((batch_size, model.hidden_dim), dtype=torch.float32)
            event = x[:, -1]  # Extract the last feature (event)
            y_pred, h = model(x, h, event)  # Do not slice x; it already contains all features
            loss = criterion(y_pred.squeeze(), y)
            loss.backward()
            optimizer.step()
            total_loss += loss.item()
        print(f"Epoch {epoch + 1}/{num_epochs}, Loss: {total_loss / len(dataloader):.4f}")

def evaluate_model(model, dataloader):
    model.eval()
    predictions, actuals = [], []
    with torch.no_grad():
        for x, y in dataloader:
            batch_size = x.size(0)
            h = torch.zeros((batch_size, model.hidden_dim), dtype=torch.float32)
            event = x[:, -1]  # Extract the event feature
            y_pred, h = model(x, h, event)  # Do not slice x
            predictions.extend(y_pred.squeeze().tolist())
            actuals.extend(y.tolist())
    return predictions, actuals

# Time Series Split and Validation
ts_split = TimeSeriesSplit(n_splits=5)
results = []

DF = feature_engineering(DF)
for fold, (train_idx, test_idx) in enumerate(ts_split.split(DF), 1):
    train_data, test_data = DF.iloc[train_idx], DF.iloc[test_idx]

    train_dataset = StockDataset(train_data)
    test_dataset = StockDataset(test_data)

    train_loader = DataLoader(train_dataset, batch_size=32, shuffle=False)
    test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)

    model = MambaExtendedNN(input_dim=5, hidden_dim=60)
    optimizer = optim.AdamW(model.parameters(), lr=0.0003, weight_decay=1e-4)
    criterion = nn.BCELoss()

    print(f"Training Model for Fold {fold}...")
    train_model(model, train_loader, optimizer, criterion, num_epochs=25)

    print(f"Evaluating Model for Fold {fold}...")
    predictions, actuals = evaluate_model(model, test_loader)

    auc = roc_auc_score(actuals, predictions)
    f1 = f1_score(actuals, np.round(predictions))
    fpr, tpr, _ = roc_curve(actuals, predictions)
    ks = max(tpr - fpr)

    results.append({"AUC": auc, "F1": f1, "KS": ks})
    print(f"Fold {fold}, AUC: {auc:.4f}, F1 Score: {f1:.4f}, KS: {ks:.4f}")
    print(f"Explanation for Traders:")
    print(
        f"In Fold {fold}, the model predicts stock price movements with an AUC of {auc:.4f}, \n"
        f"indicating a strong ability to differentiate between upward and downward movements.\n"
        f"The F1 score of {f1:.4f} reflects a balance between precision and recall, \n"
        f"while the KS statistic of {ks:.4f} indicates the maximum separation \n"
        f"between true positive and false positive rates. These metrics suggest \n"
        f"the model is highly effective in identifying trading opportunities."
    )

# Final Results
for i, result in enumerate(results, 1):
    print(f"Fold {i}: AUC={result['AUC']:.4f}, F1={result['F1']:.4f}, KS={result['KS']:.4f}")

###############Results##########################
.....
Epoch 16/25, Loss: 0.5523
Epoch 17/25, Loss: 0.5429
Epoch 18/25, Loss: 0.5430
Epoch 19/25, Loss: 0.5383
Epoch 20/25, Loss: 0.5378
Epoch 21/25, Loss: 0.5397
Epoch 22/25, Loss: 0.5340
Epoch 23/25, Loss: 0.5344
Epoch 24/25, Loss: 0.5383
Epoch 25/25, Loss: 0.5356

Evaluating Model for Fold 5...
Fold 5, AUC: 0.8370, F1 Score: 0.7368, KS: 0.5331
Explanation for Traders:
In Fold 5, the model predicts stock price movements with an AUC of 0.8370, 
indicating a strong ability to differentiate between upward and downward movements.
The F1 score of 0.7368 reflects a balance between precision and recall, 
while the KS statistic of 0.5331 indicates the maximum separation 
between true positive and false positive rates. These metrics suggest 
the model is highly effective in identifying trading opportunities.

Fold 1: AUC=0.7996, F1=0.7153, KS=0.5668
Fold 2: AUC=0.8324, F1=0.7467, KS=0.5312
Fold 3: AUC=0.7821, F1=0.6667, KS=0.4035
Fold 4: AUC=0.8532, F1=0.7413, KS=0.6179
Fold 5: AUC=0.8370, F1=0.7368, KS=0.5331

The continuous target model shows solid predictive performance, with low MSE and steadily decreasing loss, reflecting effective learning. Early predictions have higher errors, but the model improves noticeably in later folds, achieving better accuracy in stable conditions.

The binary target model performs well in classifying stock price movements, with strong AUC, F1 scores, and KS statistics, showing its ability to handle event-driven forecasting. It consistently distinguishes between price increases and declines, making it valuable for trading decisions based on market events.

Both models effectively use Mamba SSM with dynamic event conditioning, offering a flexible and robust framework for financial forecasting.

Leveraging Model Predictions for Decision-Making

The proposed model offers a powerful framework for decision-making in trading and investment, driven by its ability to forecast conditional market dynamics. By incorporating event-driven factors, F(event_tomorrow), the model enhances predictions and supports practical applications in risk management, strategy development, and market monitoring.

Event-Driven Risk Management The model's output, Y = DH(t+1) + Z, forecasts future price trends under specific conditions. For instance, if

predicts a significant price drop, traders can proactively reduce positions or hedge risks. This predictive capability also facilitates real-time risk alerts — triggering signals if price changes exceed thresholds, enabling portfolio adjustments to mitigate losses.

Developing Trading Strategies The model empowers event-driven trading strategies, such as distinguishing between "false breakouts" and genuine trend reversals when prices break support levels. If the model predicts a recovery, traders can buy the dip; if it forecasts continued decline, they can stop losses or short-sell. Moreover, the dynamic predictions allow for real-time position adjustments — scaling up during predicted growth or hedging during declines.

Enhancing Market Surveillance The model unifies predictions across multiple stocks, enabling conditional analyses for individual securities and broader sectors. For example, if most stocks in an industry break support levels and predict further declines, this could signal macroeconomic shifts. Such insights improve monitoring and strategic responses at both micro and macro levels.

Integrating into Quantitative Trading Systems The model's predictions and event factors can directly feed into quantitative trading strategies, generating buy/sell signals, defining stop-loss or take-profit levels, and improving order execution. Its precision boosts the efficiency of trading algorithms.

Commercial Applications

Portfolio Optimization: Institutions and investors can use event-driven predictions to optimize asset allocation and improve risk management.

High-Frequency Trading (HFT): The model supports real-time event monitoring and rapid strategy adjustments, ideal for HFT systems.

Enhanced Technical Analysis: Providing probabilistic forecasts and quantitative support for traditional technical indicators like support lines.

Risk Alert Systems: Designed for businesses and institutions to anticipate market volatility under specific events for credit assessments or margin management.

Data Products and APIs: Packaged as APIs or data services, the model enables integration into financial platforms, supporting ETF design or quant team strategies.

Final Thought

This paper explores an extended Mamba State Space Model (SSM) designed for event-driven forecasting, combining state-space dynamics with conditional factors inspired by Markov Decision Theory. By integrating dynamic event nodes, the model flexibly predicts both continuous targets (future prices) and binary outcomes (price movements), offering significant potential for financial applications:

• Actionable Insights: Predicting conditional probabilities aligns with traders' decision-making, offering practical guidance.
• Dynamic Adaptability: Event effects help the model adapt to market shifts and anomalies.
• Enhanced Interpretability: Explicit event modeling makes it easier to understand how triggers impact market dynamics.
• Probabilistic Forecasting: Providing probabilistic outputs reflects the uncertainty inherent in markets.

Future improvements could include more detailed event conditioning (e.g., modeling event probabilities or combining multiple triggers), enhanced state-space structures using deep neural networks for complex dynamics, multi-task learning to predict volume and volatility alongside price, and dynamic Bayesian updates for greater robustness.

Testing this approach on real-world datasets with rich macroeconomic factors and evaluating efficiency would further validate its potential. This work sets the stage for advancing event-driven forecasting in financial markets.

About me

With over 20 years of experience in software and database management and 25 years teaching IT, math, and statistics, I am a Data Scientist with extensive expertise across multiple industries.

You can connect with me at:

Email: datalev@gmail.com | LinkedIn | X/Twitter