I have written a couple of articles on the Fourier transform property of lenses, starting with this one awhile ago

They have gotten some love, so I am working on some follow up articles that goes into the details of the wave optical derivation, which compliments the original article very well since it gives justification for things I had to simply assert as true before.

In writing it up however it would be really useful, and hopefully interesting to you, to discuss the topic of Green's functions. These play an important role in optical theory, both historically and in modern approaches. Green's functions also are a fundamental object in modern quantum theory. I say that with gusto.

Green's functions really are a workhorse in modern physics, and the optics Green's functions have a beautifully intuitive interpretation The ultimate goal is to get into some of the modern topics such as optical computing and photonics, and also explore how the Fourier transform plays out in quantum mechanics. Having this jackknife available is really a must.

So I hope this article can serve as a reasonable introduction to what they are about. Mostly this will be about the math, but we'll close with how we interpret them in physics, using the example from electrostatics.

I'm of course not the first to talk about this on Cantor's paradise. Dimitri Papaioannou wrote a very nice article about them a few months back.

This article will approach the topic from a different angle, with an eye toward specific partial differential equations in physics. I think the two offer a good complement if you're new to topic of Green's functions. Enjoy.

The set the stage, imaging we're trying to solve problems of the form

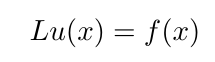
L is some linear operator, f(x) is a forcing, or source, function, and u(x) is the function we're after. By "linear," we mean that the action of L on a sum of u's is the same as the sum of L on each u(x) individually. In other words, L obeys the distributive property

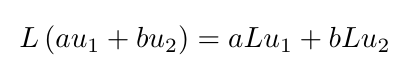
were a and b are constants. You might be thinking that the linearity condition is pretty restricting, but as it turns out phenomena in nature are linear, at least in certain regimes. Some examples are in order.

When studying electricity, we're interested in finding the electric potential energy, otherwise known as the voltage times charge, for a given charge density ρ(r), which is given by the Poisson equation

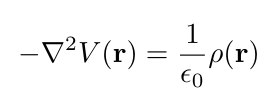
The inverse triangle symbol squared is called the Laplacian. It's defined as the sum of the second partial derivatives in each direction. It shows up quite a bit in physics, so it's worth defining it:

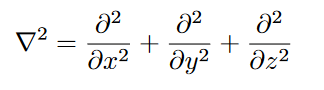
In optics we solve a similar equation, called the Helmholtz equation, where we solve for the electric field E, of a light wave with a wave vector given some source S:

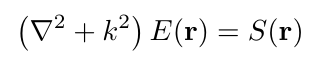
The Helmholtz equation is formally very similar to the time independent Schrödinger equation that we solve in quantum mechanics

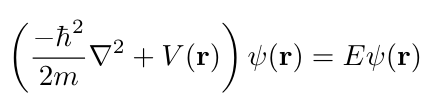
In general, solving each of these equations can be quite difficult, so it would be nice if we can solve a simpler problems. This is where Green's functions come in.

The Green's function of operator L, is a solves the related problem:

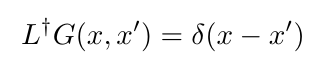
L† is the adjoint of L. We define the adjoint of an operator with something called the inner product, which we'll explain more below, but for now it is a special way of multiplying two functions. Given an L, the adjoint satisfies:

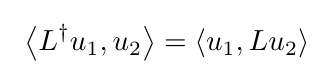
The adjoint detail is something I only actually learned recently, from this great lecture from Nathan Kutz at the University of Washington.

It's part of a series of introductory lectures he has on differential equations. Highly recommended watching.

In practice, the operators we deal with are often self-adjoint, or Hermitian.

This is the case for simple differential operators like d/dx. In quantum mechanics, any observable, which is an L that corresponds to a real measurement, is required to be self-adjoint so that measured quantities (the eigenvalues) are real.

There are exceptions. For example in modeling quantum systems that have energy dissipation or gain, we can model the change using non-Hermitian Hamiltonians, but these are pretty in infrequent. Especially if you're taking a course, all the Hamiltonians will almost surely be self-adjoint.

For self-adjoint operators, the Green's function thus also satisfies

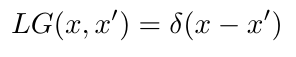
This also the most common way you'll see it defined in practice.

There's our equation, now how do we make sense of it. Since L is arbitrary, and there fore so is G, let's start with the right hand side: the delta function.

The Delta Function again

I discussed the Dirac delta function a bit in the context of the resolving power of a lens:

To recap: we define the delta function by what it does under integrals

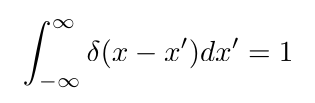
And

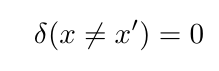
The most important fact of the delta function is the 'sifting property' when integrated against a function

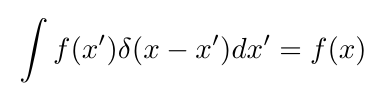
In the that article we focused on a "physical" interpretation of the delta as this infinitely dense point that arises if a lens has infinite resolving power. This made intuitive sense because we could represent the delta as a limit of gaussians or sinc functions.

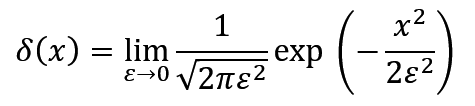
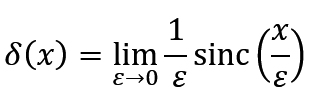
Here we'll take a different view, focusing on the sifting property specifically. To set this up, I need to introduce convolutions.

A convolution is taking in the integral between two functions, let's call them f(x) and g(x), but we offset one of the functions by some amount, which we'll call x

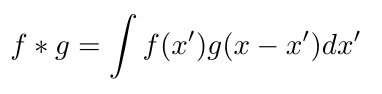
They are a way to "mix" two functions together, play a fundamental role in signal processing, and by extension machine learning, where you've probably heard of convolutional neural networks. For this discussion let's keep a ten thousand feet view, and think of convolution as a way of multiplying two functions.

I am going to claim that the convolution is like normal multiplication of numbers. We can motivate this by looking at some of the properties.

• By virtue of being an integral, convolution is linear, or obeys the distributive property:

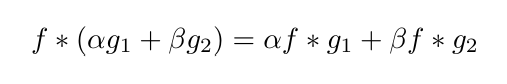
• Moreover it is commutative:

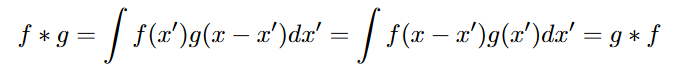
• and associative:

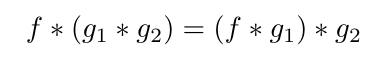
just like normal multiplication.

Moreover, the convolution of two functions is also a function, just like for numbers when we multiply two together the results is also a number.

To prove these just write down the integrals explicitly. The first two fall out immediately from the rules of calculus. The last one requires that the functions are somewhat well behaved that allows us to switch the integration order, but for physically relevant functions this will usually be the case.

However, it's not a perfect equivalence. One (large) problem is defining an inverse, the convolution analogue of a^(−1) so that a × a^(−1) = 1. In other words, how do we 'de-convolve' two functions? This problem turns out to be ill-posed in general. More on this below.

But another problem is the identity. We need something that plays role of multiplying by one. We know at f(x) × 1 = f(x) for any f, but what function I(x) satisfies: f(x) ∗ I(x) = f(x) or any f?

We already know the answer: it's the delta function.

Stare at the sifting property of the delta function (equation 11), you should recognize that it is written as a convolution. The delta function acts as the identity operator with respect to convolving two functions. In other words, the delta function is kind of like 1

In other words, the delta function is kind of like 1.

This association isn't out of nowhere. We have already seen hints of this before in the context of the Fourier transform. In the previous article on the resolution of lenses, we saw that the delta function can represented by a Fourier transform. Taking another look, we can see that the Fourier representation is has the form of taking the inverse Fourier transform of 1:

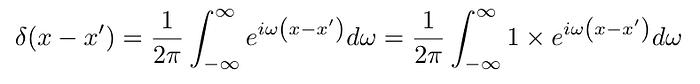
Convolutions and Inner Products

Before moving back to Green, I mentioned above that what limits our analogy to normal multiplication was the lack of a well-defined inverse. A way to see this is through one of the most common application of convolutions as "moving average" or a low-pass filter.

For example, let's take an image and convolve it with a gaussian function.

Applying a 2D convolution to an image usually blurs it significantly. It's not impossible to undo some of the blurring (deconvolution is an old topic in image processing) in practice the filtering effect of the convolution maps higher-resolution information to zero. In the language of linear algebra, there is non-trivial null-space so the operation is not invertible.

While it's not a perfect analogue of the normal product of numbers, the convolution does fit all the bills for an inner product of vectors. Without making this into a full course of linear algebra, the inner product is generalization of the dot product of the normal vectors in our 3D space.

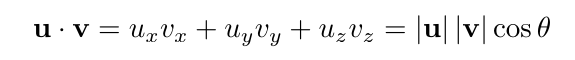
where θ is the angle between the vectors u and v.

The inner product is just a rule, or a map, to take two vectors and map them to a number. By equation 14, the rule is to take the components in each direction (x, y, z), multiply the components, and sum.

Now comparing that to the definition of the convolution in equation 12, we can see that the convolution is doing the same thing except with functions: we multiply two functions at each point and sum. More generally we define the inner product between functions f and h:

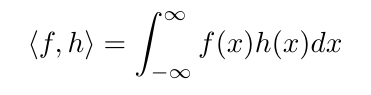
The convolution is really just the inner product in a vector space of functions, with one function shifted by an amount of our choosing. Or if you like, the convolution represents a set of inner products with some set of functions in the vectors related by shifting the function arguments.

Now in normal 3D space, we can represent any vector as a sum of the three unit vectors (vectors with length 1) in each direction, where each direction is one of our dimensions. We say that these vectors span the whole vector space, which means we can write any vector as:

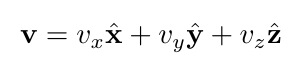
were x hat is the unit vector in the x direction. Likewise for the other directions.

We can define the components v_x, v_y, v_z as the result of taking the dot product with the unit vectors:

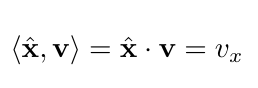
What is the equivalent of the "components" for functions? Looking at the definition of the inner product in equation 15, the component is just f(x), or the function evaluated at position x.

Here's where there is big difference for our function vector space and normal 3D space. If we're thinking of functions that are defined for all real numbers x, that means our, vectors or functions, have infinitely many components. In other words, the function vector space is has infinite dimensions.

This does introduce complications (e.g. the inner product in 15 might blow up for some functions as x -> infinity), we're going to ignore to them these details for the moment, and assume our functions are all well behaved.

With this understanding of our f(x)'s in mind, let's re-write the sifting property

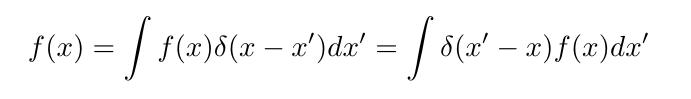
Recognizing the integral is an inner product, this is the same as:

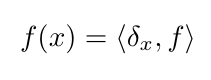
where I'm using the shorthand δ_x for the delta function at position x

Since f(x) is akin to the "component" of f as the position x, taking the inner product with the delta function centered at x is analogous to taking the dot product with a unit vector. Or to put it another way, the delta function is like a unit vector in function vector space, picking out the value, or component, at position x, just like the normal dot product in 3D space.

So let's review. we've covered two more ways to think about the delta function:

• It plays the role the identity, or multiplying by 1, for convolutions of functions. To put it another way, the delta function is kind of like 1.
• The delta function plays the role of a 'unit vector' when thinking of the vector space of functions. Taking the "dot product" with δ(x–x ′ ) gives the 'component' of the vector at the delta's position x, which is just function evaluated at x, or f(x)

One final thing: so far out discussion of inner products is with respect to real valued vectors. The extension to complex valued spaces is easy though, and just involve taking the complex conjugate of the first argument.

For functions over real variables:

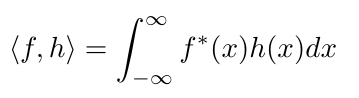
This might be a minor point, but is important when start to think about Green's functions in quantum mechanics.

Back to Green

With this understanding of the delta function, let's go back to the problem for the Green's function (equation 6).

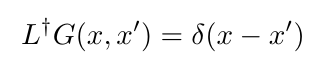
Or if our operator is self-adjoint:

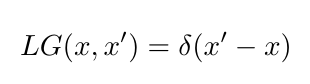
If the delta function is analogous to 1 or the identity, the Green's function seems to be analogous to the inverse of the linear operator L.

To see this more clearly let's go back to the original problem,

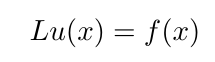
If the Green's function is analogous to the inverse of L, if we multiply by G, that is take the inner product with Green's function, we can "undo" the action of L and solve for u. So let's do it.

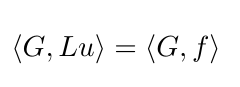
By the definition of the adjoint (equation 7), we can swap out L acting on u for the adjoint of L acting on G. And by the definition of the Green's function, this is the same as the delta function.

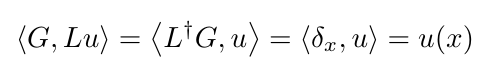
And for the right hand side:

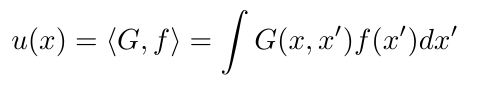
There it is. If we have the Green's function G, we solve for u by taking the integral with the source function f, analogous to multiplying f by the inverse of L.

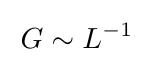
To be clear, like convolutions with normal multiplication, this is not a perfect equivalence. L can even be non-invertible, but can still have a Green's function. It's more an "operational" way of thinking about G.

You should be starting to see the power of the Green's functions. If we solve the original problem directly, we just solve for one specific source function. With the Green's function we solve for any source we choose, but "inverting" the operator L.

An important detail about Green's functions is that they are always a function of at least two arguments, that we're calling x and x′, G(x, x′ ). The Green's function seems to be a way of connecting a source at x′ to the solution at x, where we are evaluating our solution u.

This is a hint for another interpretation of the Green's functions for waves, where they play the role of a propagator. I'll go over this more in the next article. For now, put in a pin on that detail.

Looking at the right hand side of equation 22 you can see that the integral is close to the form of a convolution. It would be exact if G(x, x′ ) = G(x–x ′ ). As it turns out, this is often the case if the linear operator L has translational symmetry. This happens for instance when the operator is a sum of derivatives with constant coefficients, like the Laplacian. In these cases we have exactly a convolution.

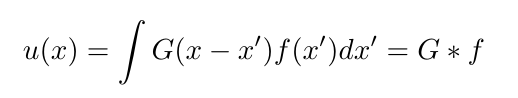
Let's Bring in the Physics

We have a math way of thinking about the Green's function as an operator's inverse, when we think of the delta as acting like 1 when we take inner products. But how do we think of the Green's function physically?

The easiest way to illustrate is with an example. Let's solve for the Green's functions for the Poisson equation (equation 3 above). Recall that we are trying to find the electric potential (voltage), given some distribution of charge in space, the latter we represent by the charge density ρ(r).

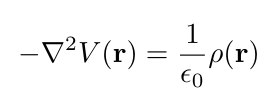
where ϵ0 is a constant called the permittivity of free space.

This is an "electrostatics" problem. We are assuming the charge is staying put. No currents are present, else we'd need to worry about the magnetic potential in addition to the electric potential to fully solve the system.

While this is a simplification, this can still be a very difficult problem, so finding the Green's function is worth the effort. More than that, this actually a physical charge distribution. If we think of an electron, as far as well know is just point with a charge -e. It's density is then

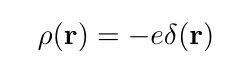
The proton by contrast is a composite particle. We could assign an effective "size" to it using quantum mechanics, but for nearly all practical purposes it likewise is just point with a positive charge +e and has the same delta function charge density.

The same consideration can be applied to whole atoms at most practical scales, e.g. a neodymium ions in your headphones or mic have an approximate charge density of

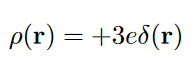
since neodymium likes to give up 3 electrons.

What this tells us is that the Green's function for the Poisson equation is the electric potential for a point charge, modulo a constant.

Since any arbitrary charge distribution is, by definition, a sum of point charges, and because the Poisson equation is linear, it follows that the potential is a sum of the Green's functions with a weighting factor ρ(r).

This is where our mathematical understanding of the delta function as a kind of "unit vector" comes in. Generally solving for the Green's function is akin to breaking up the source f(x), into a bunch of point sources, solving for the source at an arbitrary position, and then summing.

What about the solution? There is actually a slick way to solve for the Green's function for the Poisson equation using a Fourier Transform, but this article is already getting too long so I'll just quote the answer and save the details for next time.

For the Green's function we have:

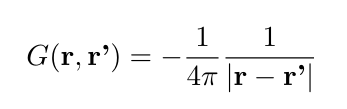
The full solution for a given ρ(r) is:

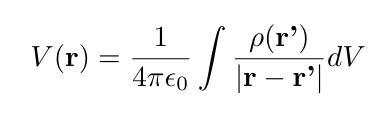
which you might recognize from a physics class.

Wrapping up

To review, the two main messages of this posts about Green's functions.

1. Mathematically Green's functions act like the inverse of the corresponding linear operator, since by taking the inner product with Lu, we solve for u
2. Physically we can interpret the Green's function as the solution for a point source, which we can sum together to form the solutions for arbitrary sources. We illustrated this by analyzing the Green's function for the Poisson equation, but it also follows for the Helmholtz equation in optics where the Green's function is the electric field of a point emitter of light.

This is a very long article, so I'll keep this closing section brief.

The only detail that I must bring up is boundary conditions, which I haven't discussed at all. Dimitri's post has me beat on that point. All the above is for Green's functions infinite space, that is where the boundary is at infinity, where all our solutions are zero. In general, of course we can have specific boundary conditions, and these conditions will change the Green's function.

I hope you found this informative, or at least mostly intelligible. Next, I plan to go into the role of the Green's function in the context of optics, then return to the Fourier transform property of lenses. Let me know your thoughts, particularly if there are any questions/topics you're curious about.

Recently made a "buy me a coffee" link. If you like this article and want more, I would very much appreciate your support. Thanks for reading. -Tom