In Chapter III, we talked about Nash Equilibria: outcomes where no one player can do better by unilaterally changing their strategy. Remember the Prisoner's Dilemma? The only Nash Equilibrium lies at defect vs. defect:

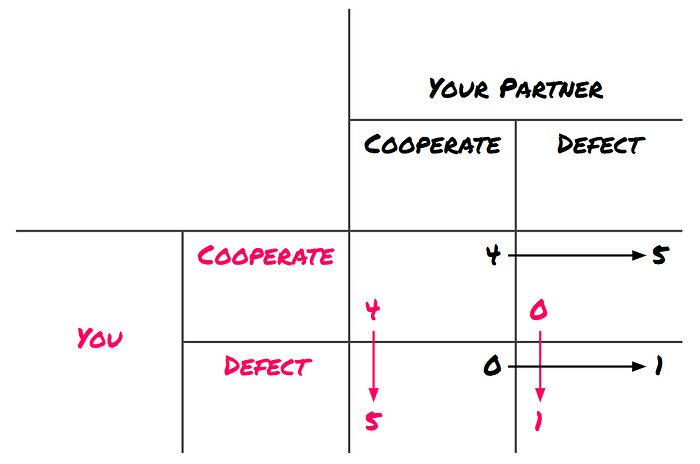
The Prisoner’s Dilemma, with the Nash Equilibrium in the defect vs. defect outcome.
The Prisoner's Dilemma

There are two important things to note about this Nash Equilibrium:

  • it's a very undesirable outcome, since there is an outcome (cooperate vs. cooperate) that is better for each player
  • it's a very "logical" situation to end up in, since both players are playing a dominant strategy.

And that's never a good combination. Of course, Nash Equilibria aren't necessarily bad. Consider the Battle of the Sexes.

Alice and Chris want to go to an event together tonight. Unfortunately, Chris has lost his phone, so they can't communicate on where to go. Earlier, they talked about both a boxing match and the ballet.

Chris would prefer to got to the boxing match, but Alice prefers the ballet. Both of them would rather go to any of the two events together than go alone to their preferred event. To which event should each of them go?

The payoff matrix for this game looks like this:

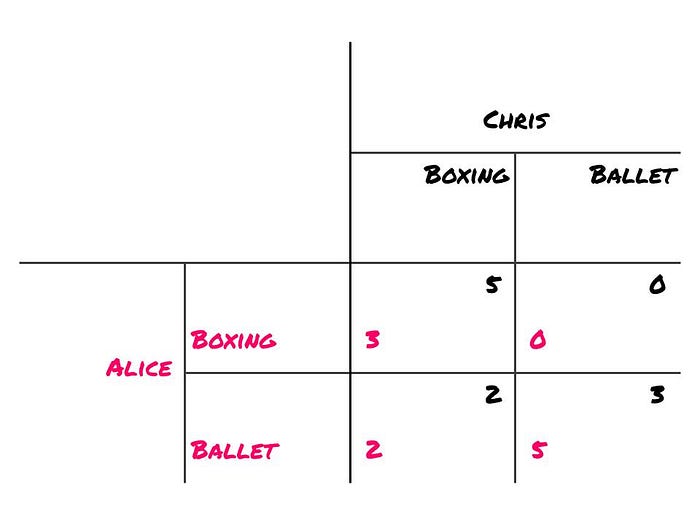
Going to the boxing match gives Alice 3 utility if Chris is there, and 0 otherwise. Going to the ballet gives her 5 utility if Chris is there, and 2 otherwise. Going to the boxing match gives Chris 5 utility if Alice is there and 2 otherwise; going to the ballet gives him 3 utility if Alice is there and 0 otherwise.
Payoff matrix for Battle of the Sexes

Alice and Chris would agree that the worst outcome is where Alice goes to the boxing match and Chris to the ballet. Conversely, if they each go to their preferred event alone, they each at least get some utility.

Both outcomes where Alice and Chris go to the same event are Nash Equilibria: in those situations, they would both lose utility if they'd unilaterally switch events.

None
Nash Equilibria in the Battle of the Sexes game

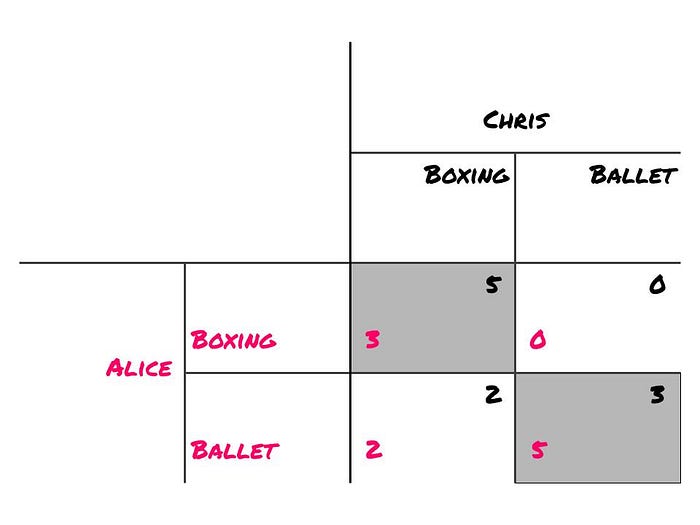
What's great about these specific Nash Equilibria is that they are also Pareto Efficient: there is no situation that's better for any player without being worse for the other. It seems these two Nash Equilibria are (by any standard) the best outcomes to the game.

Pareto Efficiency seems like a good minimum requirement for any game's outcome: if there is an outcome that's better for some player and not worse for any other player, isn't that outcome simply better?

The big problem with the Prisoner's Dilemma is that every situation except the Nash Equilibrium is Pareto Efficient. So rational and selfish players often end up in a situation that's terrible (for both of them!).

In some circumstances, bad Nash Equilibria can be avoided with some clever thinking. More on that in Chapter V!

If you would like to support Street Science, consider contributing on Patreon.