This is the third chapter in a series on Game Theory. Here are Chapter I and Chapter II.

In the previous chapter, we talked about zero-sum games: games like Tic-tac-toe, where one player's win means an equal loss for the other player.

Many real-life situations are not zero-sum. Let's consider the famous Prisoner's dilemma.

You and your partner in crime are arrested. The police have enough evidence to convict you both for a burglary (1 year in prison). They also want to punish you for a much larger crime: a bank robbery (4 years in prison). However, they don't have enough evidence for this. If only they could get you both to testify against each other. Of course, you and your partner have agreed to keep your mouths shut.

After a bit of thinking, the detectives on your case come up with the following plan. They get each of you in separate rooms, so you have no way of communicating with each other.

Each of you then gets the following deal: if you betray your partner, you — as a reward — won't get convicted for the burglary. But if your partner betrays you, you WILL get convicted for the bank robbery. What should you do, in order to minimize your prison time?

Let's get a handle on this problem. There are four possibilities:

1. You and your partner both stay silent. In that case, you both get convicted for the burglary, but not for the robbery. You each get 1 year.
2. You betray your partner, but your partner stays silent. Then your partner gets convicted for both crimes (1 + 4 = 5 years), whereas you go home free!
3. You stay silent while your partner betrays you. Then you get 5 years and your partner goes home.
4. You both betray each other. Then each of you gets convicted for the robbery, but not for the burglary. That's 4 years of prison for each of you!

In terms of utility (more is good) instead of prison time (less is good), the situation can be represented as follows:

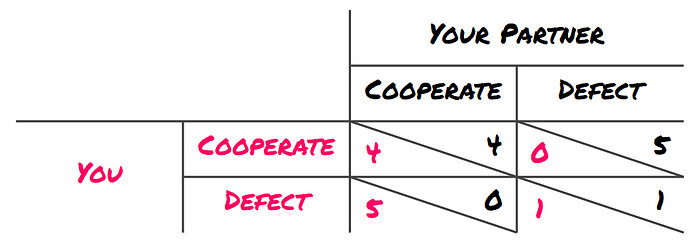
Note that this is a clear non-zero-sum game: a win for one player doesn't imply an equal loss for the other. Going from defect — defect to cooperate — cooperate gives both players 3 utility extra, for example.

Also note that you get the most utility if you defect while your partner cooperates — because you go home free. But of course, you don't know what your partner does.

However, it turns out, that doesn't matter much. If your partner cooperates, cooperating gives you 4 utility, but defecting 5. That means defecting is better given that your partner cooperates.

What about if your partner defects? Well, then defecting gives you 1 utility and cooperating 0. Defecting wins again.

So you see, defecting is best no matter what your partner does. That means defecting is a dominant strategy.

Of course, for your partner, the situation is the same. So defecting is dominant for the both of you.

From that perspective, defecting makes a lot of sense. So you both defect, getting only 1 utility (4 years in prison) each. That's so much utility left on the table! But more on that in another post.

There's something special about the situation where both of you play your dominant strategy: it's a Nash Equilibrium.

A Nash Equilibrium is a situation where none of the players can be better off by changing their strategy (while the other player(s) keep(s) their strategy).

Given that your partner defects, your best move is to defect. And given that you defect, your partner's best move is to defect:

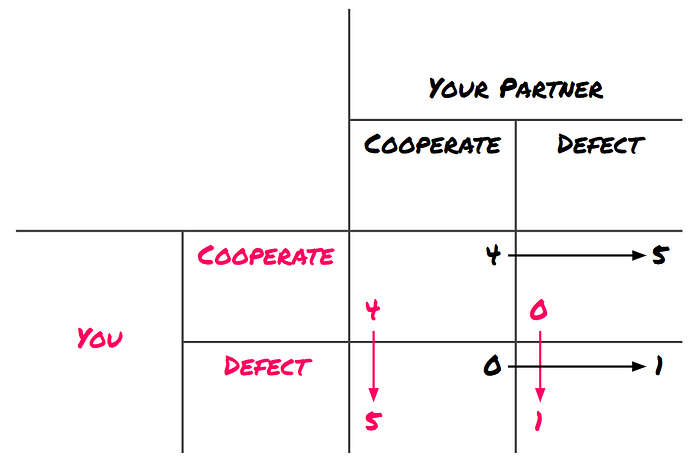
While it seems clear the optimal situation is cooperate — cooperate, it is a sad mathematical fact that the Nash Equilibrium doesn't always lie at the optimal spot.

Put more precisely, a Nash Equilibrium isn't necessarily Pareto Efficient. But more on that in the next post in this series — for now, thanks for reading!

If you would like to support Street Science, consider contributing on Patreon.