Imagine I offer you a choice between $1 and $100. Whatever you pick, you get to keep. What do you choose? (It's not a trick question.)

You pick $100, right? $100 has more value than $1 (by definition), so that's the better choice.

And what if I offer you a choice between going to the movies and cleaning a toilet?

Although this does depend on your personal preferences, you'd probably rather go to the movies. Movies are more awesome than dirty toilets. Mathematically speaking, going to the movies has more utility than cleaning the toilet.

Just like temperature measures how hot an object is, utility measures how awesome something is.

How much utility something has varies per person. For example, I might enjoy reading a popular science book, while others may call me crazy for spending my time like that.

So far, so good. Let's make things a bit more interesting.

Tic tac toe

Let's look at Tic-tac toe. For those of you who don't know this cute game, it works as follows.

We start with a square grid of 9 empty fields:

Tic-tac-toe features two players, who take turns marking one of the empty fields. One player uses X as her mark, the other uses O. The first one who gets 3 of her marks in a row (horizontally), column (vertically) or diagonal wins the game.

Tic-tac-toe is a zero-sum game, meaning a win for one of the players means an equal loss for the other player. That makes sense: once you have three in a row, you win, and your opponent loses. You can't both win. You can tie though, if all fields are filled and nobody won.

We'll look at other, non-zero-sum games later, where cooperation can play a role to make both players better off. For now, let's get back to Tic-tac-toe.

A typical game of Tic-tac-toe may start like this:

Player O might react with

After which…

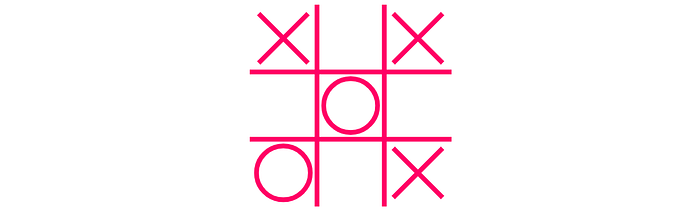
So in this game, player X wins. But the thing is: how do you decide what move to play?

In the second to last position, this was a pretty easy task for player X. There were 3 available moves (marked with 1, 2 and 3):

Move 1 doesn't do much good for player X. In fact, it gives player O the opportunity to win (at the field marked 2).

Move 3, on the other hand, is a direct win for X. Move 2 can be considered more or less neutral, as it doesn't give X a win, but also not a loss.

So we could rank these 3 moves in terms of utility as follows (though note that this is simplified):

• move 1: utility 1 (as it is a direct win)
• move 2: utility 0
• move 3: utility -1 (as it leads to a probable loss)

And so the obvious move to play is move 1.

But what about one move earlier? Remember, the situation was like this:

Player X has 5 possible moves, none of which are a direct a win. So howsss does X decide what's the best move? How should she assign utilities to the possible moves?

The problem here is that the utility of each move depends on what player O will do in her move, and, well, player X can't control (or even know!) what she will do.

In this case, the top right move is a pretty good bet, as it gives two possibilities (the shaded fields) for a win in the next move:

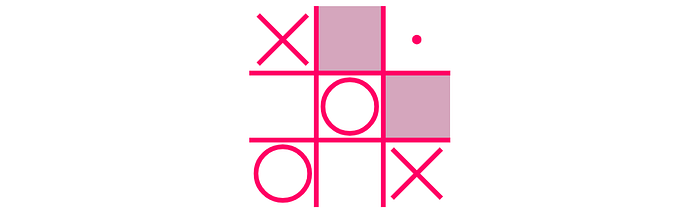
As player O can only block one of those in her next move, player X can guarantee a win like this.

But what about the first move of the game? What is the best way to start this game? That depends on what player O will do in her first move. But that probably depends on what X will do in her second move. Which depends on, well, you get the idea.

It turns out there's a very exact way to calculate the best move in any situation. Stay tuned for the next post in this series on Game theory, where we discuss the Minimax algorithm.

For now, thanks for reading!

If you would like to support Street Science, consider contributing on Patreon.